


suivant: Evènements indépendants
monter: Utilisation des probabilités conditionnelles
précédent: Exemple
- -
- Soit
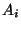 l'évènement : ``la ième boule tirée de
l'évènement : ``la ième boule tirée de 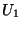 est blanche et
est blanche et 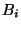 l'évènement :
``la ième boule tirée de
l'évènement :
``la ième boule tirée de 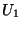 est noire''.
est noire''.
- -
- On cherche alors à calculer :
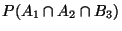 .
.
- -
- Or :
- -
- et :
- -
- d'où finalement :
Pascal Ferraro
2002-11-22