Florent
FlorentGrélard
Discrete Geometry > Bordeaux University > LaBRI florent.grelard [at] labri.fr
+33 (0)5 40 00 31 09
Research
I am working on the characterization of tubular volumes. This mainly revolves around geometrical analysis of voxel sets. I am interested in methods being applicable to concrete datasets. Below you can find explanations about our work.
New methods for the geometrical analysis of tubular organs
This paper introduces new methods to study the shape of tubular organs. Learn more
This paper summarizes and extends our cross-section estimation, skeleton refinement and skeletonization methods. Extensive comparisons between each skeleton can be obtained here.

Cross-section estimation on tubular volumes
Obtaining a precise cross-section is the critical step to perform quantitative analysis of tubular organs, for which diameter or area are often correlated to pathologies. Learn more
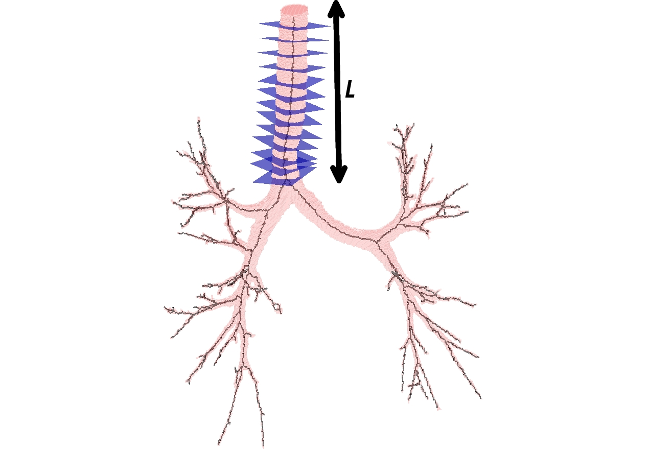
Orthogonal plane computation on a tubular volume consists in computing the 3D tangent on a discrete curve (the volume's skeleton). Various techniques exist for this purpose, but most of them are sensitive to irregularities in the curve. Moreover, they are dependent on the skeletonization algorithm. Using Voronoï Covariance Measure (VCM), we compute orthogonal planes which are robust to irregularities and noise. The idea is that the Voronoï cells are elongated in two directions (different shades of gray, see left picture): those of the basis of the orthogonal plane. Interestingly, since the VCM can be computed on any compact, it is not necessary to compute the skeleton as a first step, and orthogonal planes can be computed directly from the volume.
Centerlines of tubular volumes based on orthogonal plane estimation
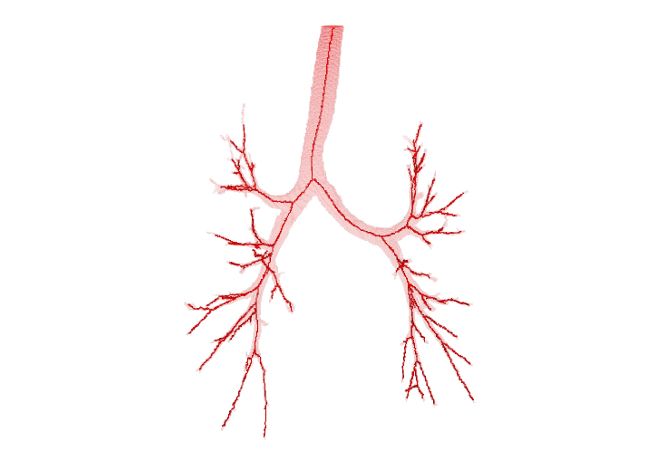
The curve-skeleton is central to many applications in discrete geometry, since it captures interesting geometrical and topological properties with respect to the initial volume. Learn more
Since orthogonal plane computation can be done on a volume, we designed a curve-skeleton algorithm. A skeleton point corresponds to a center of mass of the intersection between an orthogonal plane and the volume. The orthogonal plane also allows to track the next point (the plane normal gives this information). The rest of the algorithm is dedicated to computation efficiency, junction and end-point detection. The link to the paper can be found in the Publications tab. In the meantime, here are a few examples of resulting skeletons:

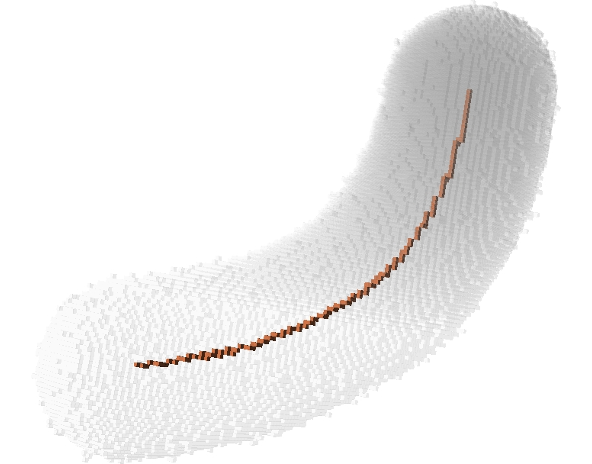

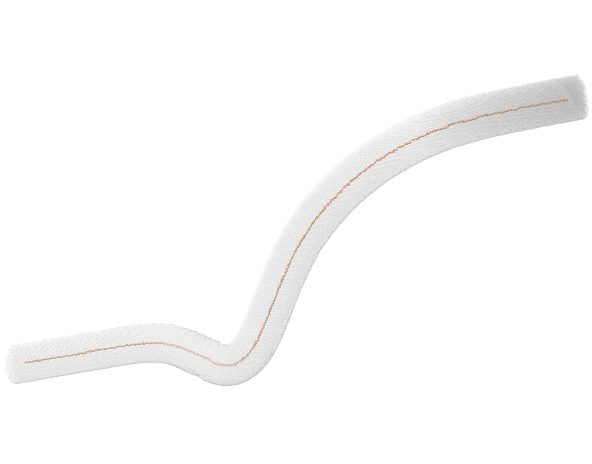
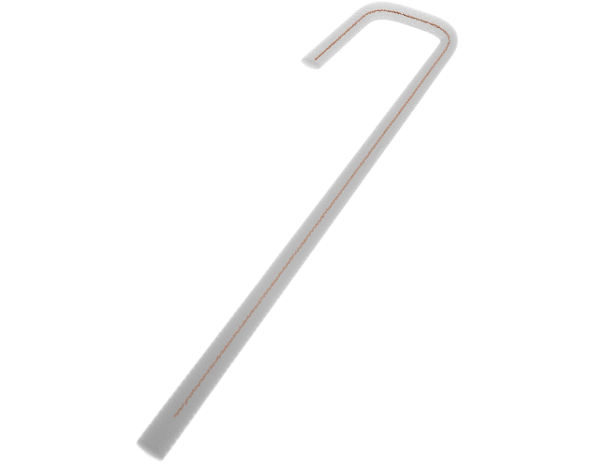
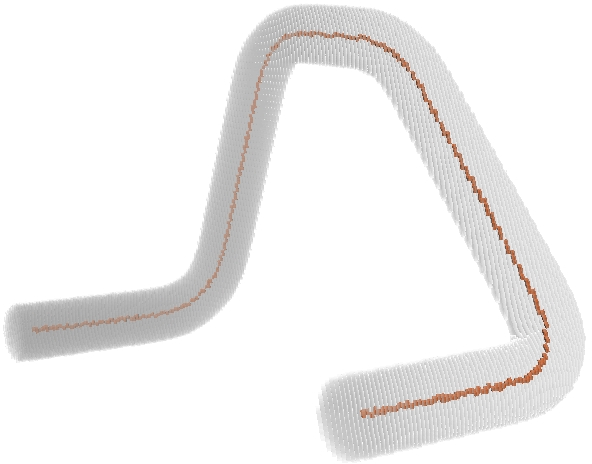
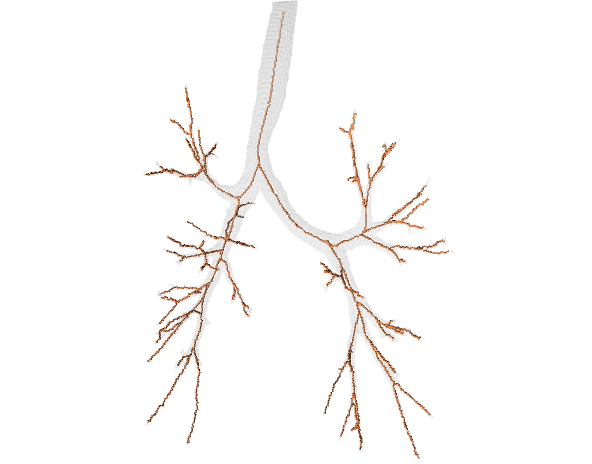
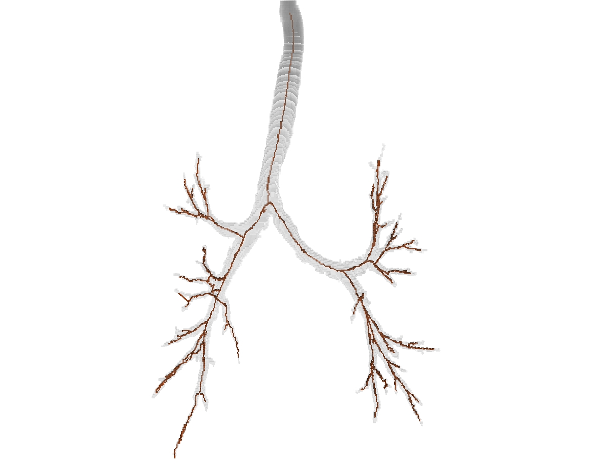
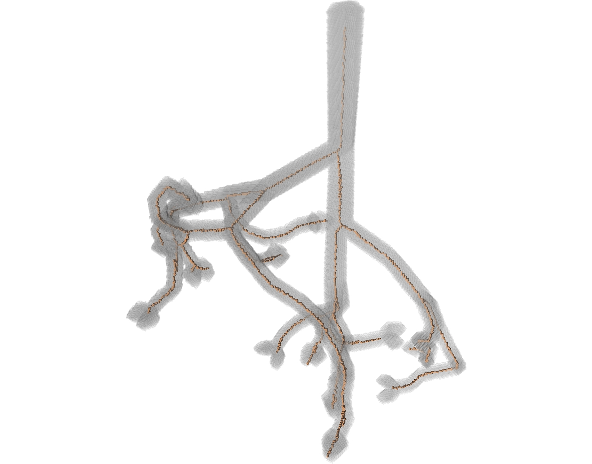
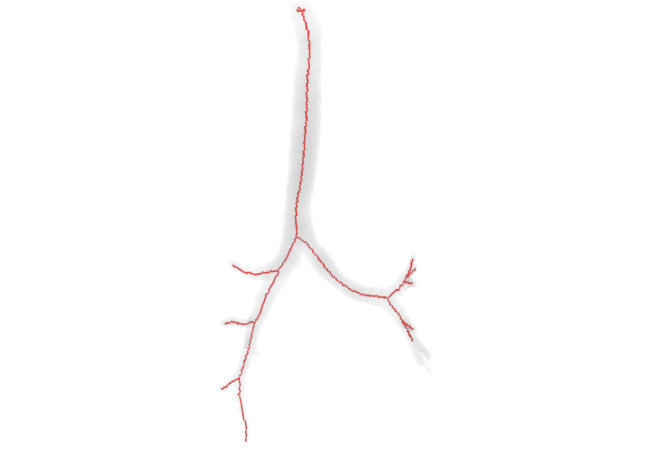
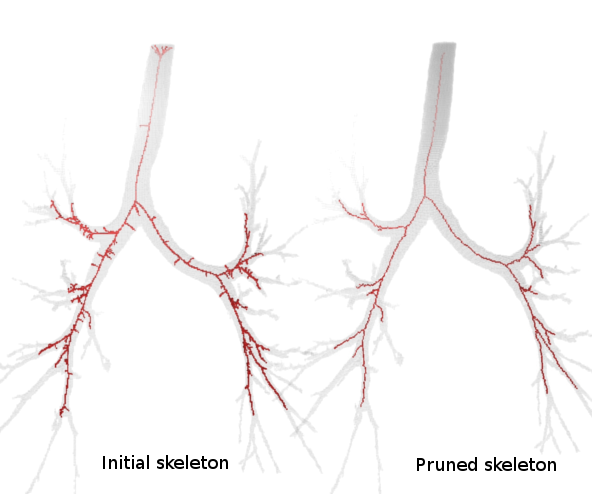
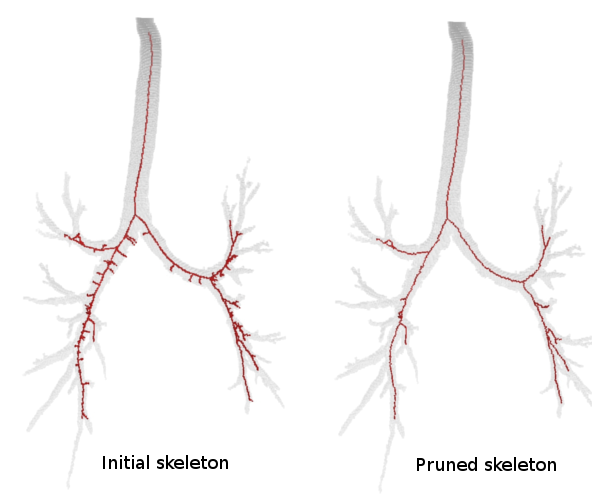
Pruning curve skeletons of tubular volumes
Many skeletonization algorithms yield spurious branches. Pruning consists in removing them. Learn more
Pruning results:
© Florent Grélard. All rights reserved | Design: HTML5 UP