Grail Help


The help file page been written for Grail 3.1.1 and contains the information you need to get started quickly. A more detailed introduction to Grail can be found in the tutorial. Clicking a hyperlink marked more information in one of the section headers for this document will take you to the corresponding section in the tutorial.
By default only Prolog files, with a .pl extension are shown in the right column. The left column shows the subdirectories of the current directory. Double-click on a filename or click on a filename and press the [Open] button to load the file.
Saving a file is done by selecting [File/Save...] from the menu. An extra confirmation is necessary to overwrite an existing file.
Pressing the left mouse button on an entry, or using the cursor keys to select the entry you're interested in, followed by <Enter> will cause the lexical graphs for this entry to appear in the ghosview window.
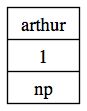 The simplest possible type of lexical entry in our grammars is an
elementary word like arthur, which we is a basic expression
of type np, for noun phrase.
The simplest possible type of lexical entry in our grammars is an
elementary word like arthur, which we is a basic expression
of type np, for noun phrase.
There is a number 1 assigned to the lexical node, which is just a unique identifier to distinguish it from all other nodes, for example from another occurrence of the same word.
Note also that the np category is on the top, indicating it is something we have as upposed to something we are searching, which would be indicated by a category at the bottom.
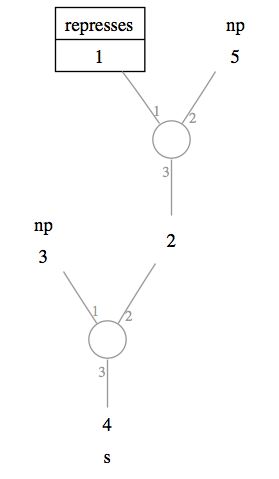 A slightly more complicated lexical entry would be given to the word
represses.
Here the result category, at the bottom, is s,
for sentence.
A slightly more complicated lexical entry would be given to the word
represses.
Here the result category, at the bottom, is s,
for sentence.
It is an incomplete lexical entry, however. It searches for two noun phrases - like the entry for arthur we have seen before - to produce this sentence.
The lexical entry here is just a tree, but there are some extra observations to make about the representation of the lexical graph.
The numbers 1 and 2 next to the connections of the two central nodes indicate the order of the two nodes at the end of this connections. This means that the np which is marked as 6 comes after the lexical anchor represses, whereas the np marked 5 will be before node 3. In this case, the left to right ordering is visible directly in the image, but the graph display algorithm can sometimes decide to portray things differently.
The label 3 to identifies the bottom (conclusion) of every link. Most of the time, however, the graph will be portrayed in such a way that this information is redundant.
Deleting an entry is done simply be selecting the word with the left mouse button or the cursor keys and then selecting [Edit/Delete Entry] from the menu. This will delete all lexical graphs for the selected word.
To assign a word to a basic category, you can simply type this category in the Formula field. You can also select previously defined basic categories by clicking on the menu arrow to the right of this text entry field.
Pressing <Enter> or selecting a category from the menu will complete the entry. Grail will ask if you want to store the entry in the lexicon. Select [Ok] to store or [Cancel] to continue editing.
The undo button  allows you to
undo your last insertion.
allows you to
undo your last insertion.
Grail allows you to make complex entries using different modes. Modes play a role not unlike that of grammatical features. The Mode entry field allows you to type in a mode or to select a mode which has been previously used in the grammar.
After having selected a mode, you have the choice of three ways of
performing a binary branching and two of performing a unary
branching. The arrow in the image indicates the position of the
current insertion point. So pressing the  button, followed by the
button, followed by the  button
will produce the tree for represses we have seen before after
inserting the appropriate simple categories using the Formula
field.
button
will produce the tree for represses we have seen before after
inserting the appropriate simple categories using the Formula
field.
There is a distinction between the white and the black connections. The black nodes have to be remove by contractions: a black and a white connection will cancel out eachother if they are connected at all nodes except the node on the black connections to which the arrow is pointing.
Like with simple entries, the undo button  allows you to remove the last connection
you have added.
allows you to remove the last connection
you have added.
By clicking on an example sentence, it will appear next to Phrase in the main window, whereas the target category will appear next Goal.
Double-clicking on an example phrase will start the parser with this sentence immediately.
Alternatively, you can enter a phrase and a goal formula yourself and then press the [Parse] button. Note that by using the small menu next to Goal you can select one of the formulas in the fragment.
Grail will search your lexicon for the words of the phrase and complain if a word does not appear there. If a similar word appears in the lexicon (different by one character or by two characters being reversed, for example) you can continue using the lexical graphs for this word instead. If you do not want this press [Cancel] and edit either you lexical or your phrase.
Grail will then show you the lexical graphs for all words and the axiom connection stage will begin.
Grail will list all possible connections which have not been tried yet in a window and allows you to select which connection to perform. Note that some fields are blank. This indicates that you have either already tried to perform this connection or that Grail has determined this connection can never be use to produce a tree: by introducing a cycle, for example.
You can reject the current lexical lookup altogether by closing the window. This will cause Grail to search for alternate lexical entries or to fail if all alternatives have already been tried.
After all formulas have been connected Grail will perform the structural rewrites.
Grail will perform the structural rules permitted by your fragment automatically and give a single representation for all the structural possibilities. In this graph there can be multiple connections going up from a single node, which will represent a choice between several trees.
If this graph gets too dense, you might prefer to change the graph mode in [Options/Graph Mode] to distributed.
When there are multiple active constructors, you can select which one to contact. Be aware that selecting the wrong contraction can lead to a dead end, so plan ahead when selecting the contractions.
Performing a contraction can make new structural rewrites possible. So after each contraction Grail will perform any new rewrites and give you a new choice for a contraction.
Finally, when all contractions have been performed, Grail will perform the structural rewrites once more. The graph will be a representation of al structural configurations - including word order - for the current reading of the phrase.
If alternate untried axiom links exist, you will be given the opportunity to try and generate a different solution.
