Algebraic Point Set Surfaces
Siggraph 2007, San-Diego, US.
Abstract
In this paper we present a new Point Set Surface (PSS) definition based on moving least squares (MLS) fitting of algebraic spheres. Our surface representation can be expressed by either a projection procedure or in implicit form. The central advantages of our approach compared to existing planar MLS include significantly improved stability of the projection under low sampling rates and in the presence of high curvature. The method can approximate or interpolate the input point set and naturally handles planar point clouds. In addition, our approach provides a reliable estimate of the mean curvature of the surface at no additional cost and allows for the robust handling of sharp features and boundaries. It processes a simple point set as input, but can also take significant advantage of surface normals to improve robustness, quality and performance. We also present an novel normal estimation procedure which exploits the properties of the spherical fit for both direction estimation and orientation propagation. Very efficient computational procedures enable us to compute the algebraic sphere fitting with up to 40 million points per second on latest generation GPUs.
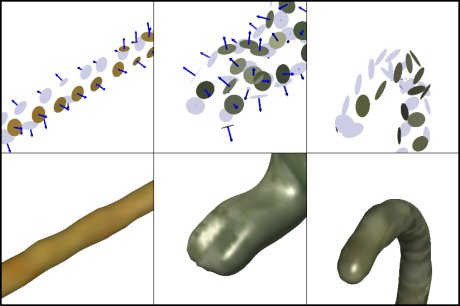
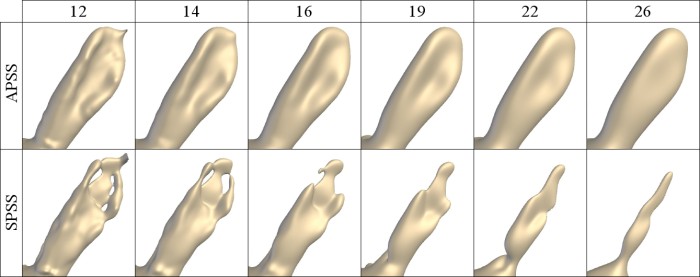
Additional pictures

Left: initial dense chameleon model from which 4k samples have been uniformly picked (depicted with red dots, top) and APSS reconstruction (bottom). Click to enlarge. Right: close up view of the 4k samples model (top) and the APSS reconstruction (bottom).
Comparison of the reconstruction with sphere fit (top row) and plane fit (bottom row) of a low sampled model using various weight radii.
