Planar maps weighted by their Potts polynomial, divided by q.
Catalytic variables: x (degree of the root vertex) and y (degree of the root face).
Other variables: t (edges), w (non-root vertices) and z (non-root faces).
Finally, nu counts monochromatic edges, and q is the number of colors.
| > | restart: |
The equation of Proposition 1.
| > | eqM:=1+x*y*w*t*((nu-1)*(y-1)+q*y)*M(x,y)*M(1,y) + x*y*z*t*(x*nu-1)*M(x,y)*M(x,1) +x*y*w*t*(nu-1)*(x*M(x,y)-M(1,y))/(x-1)+ x*y*z*t*(y*M(x,y)-M(x,1))/(y-1)-M(x,y); |
![]()
![]()
Expansion of the series M
| > | Mser:=proc(n) option remember: if n=0 then 1 else factor(series(subs(M(x,y)=Mser(n-1), M(x,1)=subs(y=1,Mser(n-1)), M(1,y)=subs(x=1,Mser(n-1)) ,eqM+M(x,y)),t,n+1)); fi:end: |
| > | Mser(1); |
![]()
For one-edge maps, one should find:
(q-1 + nu) w x y^2 for the isthmus (2 vertices, degree 1 for the root-vertex, degree 2 for the root face)
nu x^2 y z for the loop (2 faces, degree 2 for the root-vertex, degree 1 for the root face).
Let us check.
| > | normal((q-1+nu)*w*x*y^2+nu*x^2*y*z-coeff(Mser(1),t)); |
![]()
| > |
| > |
| > |
| > |
From now on, we set z, the face variable, to 1.
| > | eqM:=subs(z=1,eqM); |
![]()
![]()
Expansion of the series M
| > | Mser:=proc(n) option remember: if n=0 then 1 else factor(series(subs(M(x,y)=Mser(n-1), M(x,1)=subs(y=1,Mser(n-1)), M(1,y)=subs(x=1,Mser(n-1)) ,eqM+M(x,y)),t,n+1)); fi:end: |
| > | Mser(1); |
![]()
| > |
| > |
The kernel
| > | Ker:=-coeff(eqM,M(x,y)); |
![]()
The right-hand side
| > | R:=coeff(eqM,M(x,y),0); |
![]()
How many roots has Ker (when solved for y)? There exists only one power series in t, denoted Y_1, that cancels Ker.
| > | factor(subs(t=0,numer(Ker))); |
![]()
To obtain another root, we have to set x=1+t*s
| > | factor(subs(t=0,numer(subs(x=1+t*s,Ker)))); |
![]()
| > | factor([solve(%,y)]); |
![]()
Expansion of the series Y_i (Lemma 5). We replace M by its expansion (first terms) and then solve for y, using the package GFUN (available in the Algolib library).
| > | n:=6: res:=normal(subs(M(1,y)=convert(subs(x=1,Mser(n)),polynom), M(x,1)=convert(subs(y=1,Mser(n)),polynom),x=1+t*s,numer(Ker))): |
| > |
| > | with(gfun): |
| > | algeqtoseries(res,t,y,2,true); |
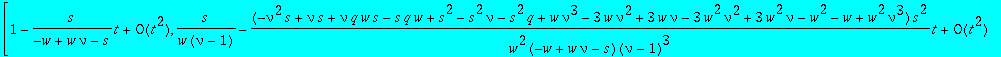
![]()
| > |
| > |
| > |
The case q=2 et nu=0 (Section 2)
| > |
| > |
Construction of the two invariants (Section 6)
| > |
The two invariants. The first one is I1:
| > | I1:=y*t*w*q*M(1,y)-(1-y)/y+t*y/(y-1); |
![]()
The second is J=CC^(m/2) T_m(xsubs) with
| > | xsubs:=-1/2*(nu-1)*(q-4)/C^(1/2)*yinv+1/2*(-2+2*nu+q)/C^(1/2)*II+1/2*(-2*q-4*nu+4+q*nu)/C^(1/2); |
![]()
| > | CC:=(-2*nu+q*nu+1+nu^2)*II^2-q*(nu+1)*II+(nu-1)*(q-4)*(w*q+nu-1)*t+q; |
![]()
| > |
| > |
The case q=1 (m=3, k=1) (Section 10.1)
| > |
| > |
| > |
A derivative we have to evaluate in Lemma 17
| > |
| > |
| > |
The case q=2 (m=4,k=1) (Section 12.1)
| > |
| > |
The case q=3 (m=6,k=1) : an equation with a single catalytic variable (Section 13.1)
| > |
| > |
Interlude : planar maps by guessing and checking (Section 13.1, continued)
| > |
The case q=3 and nu=0 : guessing the three unknown series M(1), M'(1) and M"(1) (Section 13.1, continued)
| > |
| > |
The case q=3 and nu=0 : conclusion (Section 13.1, the end)
| > |
| > |
| > |
The case q=3 and nu=0 : asymptotics (Theorem 25)
| > |
| > |
| > |
| > |
From separable maps to non-separable ones (Section 14.1)
| > |