Définition 1
Une expérience aléatoire
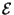
est une expérience qui,
répétée dans des conditions apparemment identiques, peut conduire
à des résultats différents.
Définition 2
Soit
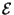
une expérience aléatoire et
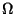
l'univers
qui lui est associé. On dit qu'un évènement est lié à l'expérience
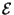
si pour tout résultat
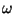
de
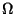
, on sait
dire si cet évènement a eu lieu ou non.
Exemple 1
On lance deux dés cubiques discernables. L'ensemble des résultats
est alors l'ensemble des couples d'entiers compris entre 1 et 6 :
Déterminer la représentation de l'évènement : ``
La somme des
points est supérieure ou égale à 10''.
![]() est noté
est noté
![]() et s'apelle l'univers associé à
et s'apelle l'univers associé à
![]() .
.
![]() : ``La somme des
points est supérieure ou égale à 10'' est représentée par :
: ``La somme des
points est supérieure ou égale à 10'' est représentée par :