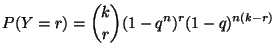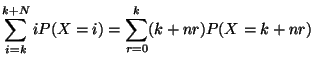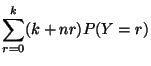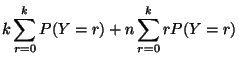suivant: translation d'une loi Binomiale
monter: Loi Binomiale
précédent: Exemple d'application
- -
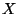 désigne la variable aléatoire: ``Nombre d'analyses
effectuées'';
désigne la variable aléatoire: ``Nombre d'analyses
effectuées'';
- -
- Pour chaque groupe,
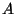 est l'évènement : ``Un, au
moins des échantillons contient
est l'évènement : ``Un, au
moins des échantillons contient 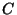 ''.
''.
- -
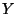 désigne la variable aléatoire: ``Nombre de
réalisation de
désigne la variable aléatoire: ``Nombre de
réalisation de 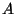 dans les
dans les 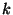 groupes.
groupes.
- -
- On a :
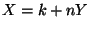
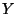 suit la loi binomiale
suit la loi binomiale
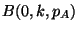
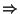 Déterminer
Déterminer 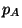 et en déduire les caractéristiques de
et en déduire les caractéristiques de 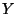 puis de
puis de 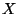 .
.
La probabilité qu'aucun des 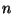 échantillons d'un goupe ne contienne
le corps
échantillons d'un goupe ne contienne
le corps 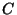 est :
est :
D'où :
Alors :
Comme 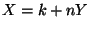 , on a
, on a
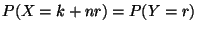 , d'où :
, d'où :
Prenons par exemple 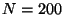 ,
, 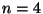 ,
, 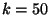 et
et 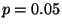 Avec
Avec 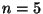 , on a :
Le gain de travail, grâce à ce protocole est, en moyenne, très
important lorsque
, on a :
Le gain de travail, grâce à ce protocole est, en moyenne, très
important lorsque 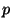 est petite.
est petite.



suivant: translation d'une loi Binomiale
monter: Loi Binomiale
précédent: Exemple d'application
Pascal Ferraro
2002-11-22
![]() échantillons d'un goupe ne contienne
le corps
échantillons d'un goupe ne contienne
le corps ![]() est :
est :