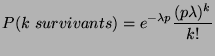Le nombre d'oeufs pondus est supérieur (ou égal) à ![]() .
.
On suppose que l'insecte ponds ![]() oeufs, avec
oeufs, avec ![]() .
.
La probabilité pour que l'insecte ponde ![]() oeufs est :
oeufs est :
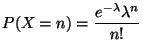
Soit ![]() la variable aléatoire : nombre d'oeufs qui se développent
parmi
la variable aléatoire : nombre d'oeufs qui se développent
parmi ![]() oeufs pondus.
oeufs pondus.
Soit ![]() l'évènement:''l'oeuf considérer se développe''.
l'évènement:''l'oeuf considérer se développe''.
![]() suit une loi binomiale
suit une loi binomiale ![]() , d'où :
, d'où :
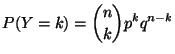
La probabilité pour que l'insecte ponde ![]() oeufs et que parmi ces
oeufs et que parmi ces
![]() oeufs,
oeufs, ![]() se développe est :
se développe est :
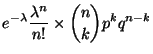
On considère l'évènement: ``![]() oeufs survivent.''
oeufs survivent.''
Cet évènement peut se réalsier d'une infinité de manières:
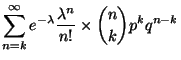 |
|||
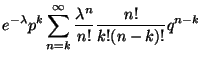 |
|||
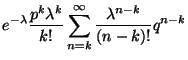 |
|||
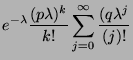 |
|||
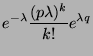 |
|||
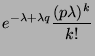 |
|||
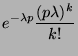 |
Il s'agit donc d'une loi de poisson de paramètre ![]()