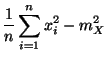suivant: Loi de Bernoulli
monter: Loi discrète uniforme
précédent: Exemple d'application
- -
- Les femelles peuvent produire 4 types d'allèles :
- -
- Les mâles ne peuvent fournir qu'un seul phénotype :
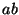 .
.
- -
- Les constitutions génétiques des descendants sont donc :
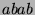 , ou encore
, ou encore 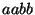 , soit
, soit 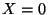 ,
,
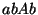 , ou encore
, ou encore 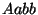 , soit
, soit 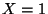 ,
,
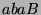 , ou encore
, ou encore 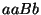 , soit
, soit 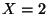 ,
,
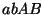 , ou encore
, ou encore 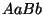 , soit
, soit 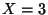 .
.
Chacun des génotypes a la même probabilité d'apparition chez un
descendant :
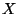 suit donc une loi uniforme de probabilité
suit donc une loi uniforme de probabilité
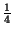 d'où :
d'où :
- -
- Le nombre moyen de rayures par animal descendants est :
- -
- La variance est :



suivant: Loi de Bernoulli
monter: Loi discrète uniforme
précédent: Exemple d'application
Pascal Ferraro
2002-11-22
![\includegraphics*[width=4cm]{/usr/labri/ferraro/Enseignement/DESS/Cours/Chap1_lois_discretes/geno.eps}](img37.png)
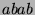 , ou encore
, ou encore 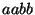 , soit
, soit 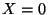 ,
,
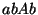 , ou encore
, ou encore 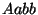 , soit
, soit 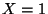 ,
,
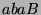 , ou encore
, ou encore 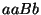 , soit
, soit 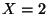 ,
,
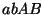 , ou encore
, ou encore 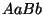 , soit
, soit 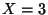 .
.
![\includegraphics*[width=4cm]{/usr/labri/ferraro/Enseignement/DESS/Cours/Chap1_lois_discretes/geno.eps}](img37.png)
![]() suit donc une loi uniforme de probabilité
suit donc une loi uniforme de probabilité
![]() d'où :
d'où :