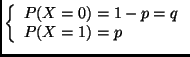Définition 2
Soit une expérience dont le résultat est aléatoire et soit
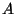
un
évènement défini sur cette expérience. Soit
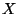
la variable
aléatoire prenant la valeur
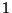
quand
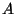
est réalisé et 0 quand
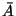
est réalisé. On dit que
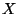
est une
variable de
Bernoulli s'il existe
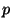
et
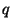
dans
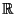
vérifiant :
On dit également que
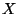
suit une loi de Bernoulli
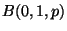
.