TD5 : Passage à la 3D
1 - Transformations
Redimensionner, déplacer, faire tourner une forme en modifiant individuellement et manuellement ses sommets est laborieux, alors qu'une transformation géométrique globale pourrait être utilisée. Cette transformation peut être représentée par une matrice 4x4 (en coordonnées homogènes) ; nous utiliserons à nouveau l'implémentation fournie par la librairie Eigen dont voici un aide-mémoire.
| GLSL | C++ (Eigen) | |
|---|---|---|
| vecteur 2D | vec2 | Vector2f |
| vecteur 3D | vec3 | Vector3f |
| vecteur 4D | vec4 | Vector4f |
| matrice 2x2 | mat2 | Matrix2f |
| matrice 3x3 | mat3 | Matrix3f |
| matrice 4x4 | mat4 | Matrix4f |
| matrice 3x4 | mat3x4 | Matrix<float,3,4> |
| accès | v.x | v.x(), v[0], v(0) |
| v.y | v.y(), v[1], v(1) | |
| v.z | v.z(), v[2], v(2) | |
| v.w | v.w(), v[3], v(3) | |
| (i=ligne,j=colonne) | M[j][i] | M(i,j) |
| colonne d'une matrice | M[j] | M.col(j) |
| ligne d'une matrice | M.row(i) | |
| sous-matrice | M.block(i,j,rows,cols) |
| GLSL | C++ (Eigen) | |
|---|---|---|
| produits | M * v | M * v |
| matriciels | M1 * M2 | M1 * M2 |
| transpose | transpose(M) | M.transpose() |
| produit scalaire | dot(v1,v2) | v1.dot(v2) |
| norme | length(v) | v.norm() |
| produit vectoriel | cross(v1,v2) | v1.cross(v2) |
| translation d'un vecteur v | Translation3f(v) | |
| rotation d'un angle theta autour de v | AngleAxisf(theta,v) | |
| mise à l'échelle d'un facteur s | Scaling(s) | |
| transformation affine | Affine3f A; | |
| partie linéaire 3x3 | A.linear() | |
| translation | A.translation() | |
| matrice 4x4 | A.matrix() |
Exemple d'utilisation :
Affine3f A;
A = Translation3f(p) * AngleAxisf(theta,v) * Translation3f(-p);
v2 = A * v1;
1. Ajoutez une variable uniforme de type mat4 au vertex shader et passez lui une homothétie de facteur 1/2 dans Viewer::display (à l'aide des fonctions glUniformMatrix4fv et Shader::getUniformLocation). Transformez la position du vertex par cette matrice. Côté C++, vous pouvez utiliser une variable de type Eigen::Affine3f pour stocker cette transformation ; il faudra alors faire appel aux méthodes matrix() et data() pour obtenir le pointeur sur les données à passer au shader. Utilisez le clavier pour contrôler le facteur de zoom.
2. Expérimentez et combinez d'autres transformations planaires (rotations, translations). Notez l'importance de l'ordre de ces transformations en inversant translation et rotation. Attention, pour l'instant la zone visible sur chaque axe va de -1 à 1.
3. Intégrez à votre code les classes Shape, Cube et Sphere ci-jointe (ajoutez les au CMakeLists.txt). Ajoutez une instance de Cube au Viewer, initialisez ses VAO/VBO en appelant sa méthode Cube::init, puis affichez le cube dans la méthode display. Une seule face du cube est actuellement visible.
2 - Caméra
1. Pour passer d'un espace 2D à 3D, il nous faut définir une matrice de projection. Intégrez la classe Camera ci-jointe à votre code, et créez une matrice de projection perspective avec sa méthode :
Matrix4f Camera::perspective(float fovy, float aspect, float zNear, float zFar);
Vous constaterez que l'affichage est étrange : l'élimination des parties cachées n'est pas correcte. Activez le depth buffer avant la boucle de rendu (état GL_DEPTH_TEST), et videz le à chaque appel de Viewer::display avec glClear(GL_DEPTH_BUFFER_BIT).
2. Il est pratique de contrôler la caméra en lui indiquant une position d'observation position, une cible à viser target et une orientation verticale up. Implémentez la fonction générant ainsi la matrice de vue, avec ce prototype :
Matrix4f Camera::lookAt(const Vector3f& position, const Vector3f& target, const Vector3f& up);Indices : vous devez construire une base orthonormale 3D dont le premier axe $\vx{z}$ est l'opposé du vecteur de visée. Le deuxième axe $\vx{y}$ correspond au vecteur dans le plan défini par l'orientation verticale up et la direction de visée qui est orthogonal au premier axe. Le dernier axe $\vx{x}$ du repère peut finalement être obtenu par produit vectoriel entre les deux vecteurs précédent. Assemblez alors la matrice 4x4 de changement de base à partir de ces vecteurs en n'oubliant pas que le repère doit être centré sur la position d'observation.
3. Il est courant de séparer la transformation des objets de celle fixant le point de vue de la caméra dans la scène. Déclarez une nouvelle matrice en attribut de la classe Shape où vous y stockerez la transformation de chaque objet. Modifiez le
4. Permettez le contrôle de la caméra à l'aide des touches du clavier : rotation horizontale et verticale autour du point visé, et translation dans la direction de visée.
3 - Système solaire
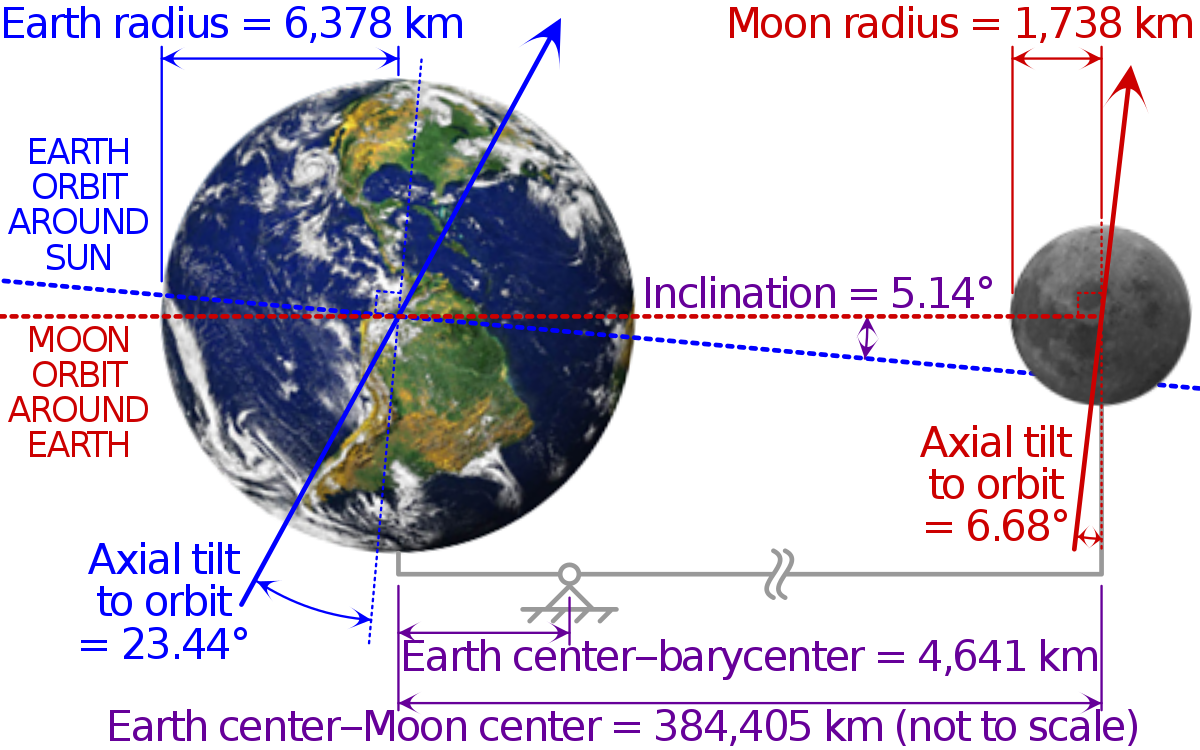
Pour appliquer les concepts précédents à un cas concret, vous allez mettre en œuvre un mini système solaire animé. Il inclura au moins la terre, qui devra tourner sur son axe et être en révolution autour du soleil. Vous ajouterez ensuite notre lune en révolution autour de la terre.
1. Commencez par un système solaire minimaliste avec une sphère (classe Sphere) au centre de la scène représentant le soleil et une seconde sphère, plus petite, tournant autour du soleil à une distance fixe.
Conseil : Vous pouvez modifier les
2. Faites en sorte que la terre tourne sur elle-même autour d'un second axe. Modifiez l'axe de la terre afin que son axe de rotation soit incliné (d'environ 23 degrés) comme c'est le cas en réalité. Vous pouvez utiliser la classe Eigen::AngleAxis pour effectuer une rotation autour d'un axe arbitraire.
3. Sur le même principe, ajoutez une lune tournant autour de la terre.
Vous pouvez continuer en ajoutant d'autres planètes et leurs lunes pour former le système solaire complet.