TD4 - Échantillonnage
L'intégration de Monte-Carlo est au cœur de nombreux algorithmes de synthèse d'image photo-réalistes. Dans ce TD, après un échauffement en 1D, vous l'utiliserez dans le cas de l'anti-aliasing en sur-échantillonnant les pixels et dans le cas des sources étendus pour obtenir des ombres douces.
1. Intégration de Monte-Carlo 1D
L'objectif est de calculer l'intégrale de la fonction 1D : $f(x) = 5x^4$ sur l'intervalle $[0,1]$, c'est-à-dire $I = \int_0^1 5x^4 dx$. Téléchargez l'archive MonteCarlo.zip et compilez son contenu. Implémentez la fonction int_mc qui doit retourner l'estimation de l'intégrale selon l'estimateur de Monte-Carlo $\langle I \rangle$ avec une densité de probabilité uniforme $(\forall i,~pdf(x_i)=1)$, soit :
$$\langle I \rangle = \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{pdf(x_i)} = \frac{1}{N} \sum_{i=1}^N 5x_i^4$$
Ignorez pour l'instant la variable de sortie varest.
Le main appelle int_mc avec un nombre croissant d'échantillons puis dessine avec gnuplot l'erreur d'estimation en fonction de $N$. Exécutez plusieurs fois le programme et comparez les tracés.
Calculez maintenant la variance analytique en fonction de N : $$\sigma^2_{est} = \frac{1}{N} \int_0^1 \left(\frac{f(x)}{pdf(x)} - I \right)^2 pdf(x) dx = \frac{1}{N} \int_0^1 (5x^4 - 1)^2 dx$$ Tracez sur le graphique précédent cette variance.
Estimez enfin la variance numérique (variable de sortie varest) à l'aide de l'estimateur :
$$ \langle \sigma^2_{est} \rangle = \frac{1}{N-1} \left\{ \frac{1}{N} \sum_{i=1}^N \left(\frac{f(x_i)}{pdf(x_i)}\right)^2 - \left( \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{pdf(x_i)}\right)^2 \right\} $$
Affichez-la sur le même graphique.
2. Anti-Aliasing
Les silhouettes des objets et les textures souffrent clairement de problèmes d'aliasing. Pour le résoudre, il faut intégrer la radiance sur le pixel, ce que l'on peut faire au sens de Monte-Carlo en lançant plusieurs rayons par pixel et en moyennant leur contribution.
2.1. Échantillonnage régulier
Modifiez la méthode Viewer::renderBlock pour qu'elle lance plusieurs rayons par pixel à travers une grille régulière de taille $n \times n$, où $n$ correspondra à l'attribut sampleCount de la caméra (lu depuis le fichier de scène). Vous devriez obtenir le résultat suivant avec "tw.scn" en fixant le nombre d'échantillons à 8 dans le fichier de scène :

2.2. Échantillonnage stratifié
Implémentez ensuite un échantillonnage stratifié en ajoutant du jitter à chaque rayon. Vous pouvez utiliser la fonction :
Eigen::internal::random<float>(a,b)pour obtenir un nombre aléatoire entre a et b. Activez la stratification lorsque Camera::isStratified() renvoie true (également lu depuis le fichier de scène).

La scène "deuxSpheres.scn" est particulièrement difficile en raison de la texture en damiers du plan infini :
 |
 |
 |
 |
2.3. Bonus : filtre de reconstruction
On peut encore améliorer les résultats en pondérant la contribution des rayons correspondant à un pixel par un filtre de reconstruction, par exemple par un noyau gaussien (centré sur le milieu du pixel). Pour plus de flexibilité, vous pouvez coder une classe Filter qui donnera les poids ainsi que les décalages (par rapport au centre du pixel) associés à chaque rayon.
3. Sources étendues
Les sources ponctuelles et directionnelles sont rarement physiquement réalistes. La majorité des sources lumineuses est surfacique. Calculez les ombres portées pour de telles sources étendues nécessite cependant d'intégrer leur visibilité depuis le point d'évaluation. Pour ce faire, vous utiliserez à nouveau un échantillonnage de Monte-Carlo.
Parcourez la classe AreaLight représentant une source lumineuse étendue rectangulaire, potentiellement texturée. Analysez en particulier la méthode :
Color3f AreaLight::intensity(const Point3f &x, const Point3f &y) const
3.1. Échantillonnage de Monte-Carlo
Modifiez l'intégrateur de Whitted pour tirer un rayon d'ombre dans une direction aléatoire vers la source étendue. Pour déterminer cette position, utilisez les vecteurs unitaires AreaLight::uVec et AreaLight::vVec ainsi que la position et la taille de la source. Notez que l'on peut détecter qu'une Light est une AreaLight avec un dynamic_cast :
1
2
3
4
5
6
7
8
9
if(dynamic_cast<const AreaLight*>(lights[i]))
{
const AreaLight* light = dynamic_cast<const AreaLight*>(lights[i]);
// source étendue
}
else
{
// lampe ponctuelle ou directionnelle
}
Vous devriez obtenir ce type de résultat pour la scène "tw_area.scn" :

Testez également avec la scène "killeroo_area.scn" :


3.2. Source texturée
On veut moduler l'intensité de la source étendue par la texture "light_source.exr".

Pour cela, modifiez AreaLight::intensity pour accéder à l'attribut Bitmap m_texture. Ajoutez également la ligne suivante au fichier de scène "tw_area.scn" :
<light type="areaLight">
<string name="texture" value="light_source.exr" />
<!-- le reste est identique -->
</light>Avant de tester, essayez de prédire quel sera le résultat ...afficher le résultat :


3.3. Bonus : échantillonnage stratifié
Les ombres douces générées sont très bruitées car, si l'échantillonnage des pixel est stratifié, celui de la source étendue est purement aléatoire. À titre de comparaison, implémentez l'échantillonnage stratifié de la lampe en tirant $n \times n$ rayons d'ombres sur une grille avec du jittering. Pour que la comparaison des ombres soit juste, n'utilisez qu'un rayon par pixel.
Vous devriez obtenir ce résultat pour "tw_area.scn" :

...et pour "killeroo_area.scn" :

Il est évidemment possible de combiner les deux approches, puis d'ajuster le nombre d'échantillons par pixel et par source étendue pour obtenir la qualité souhaitée.

4. Ambiante Occlusion
L'ambiant occlusion est une technique de rendu faisant l'hypothèse qu'une surface (diffuse) reçoit une illumination uniforme depuis toutes les directions et que la visibilité est le seul effet important. Certaines portions de la surface vont recevoir moins de lumière que d'autres en raison des occlusions, et donc apparaître plus sombres. Formellement, l'ambiant occlusion $L$ au point $\vec{x}$ est l'intégrale de la fonction de visibilité $V$ sur l’hémisphère supérieur centré en ce point :
$$L(\vec{x}) = \int_{\Omega}V(\vec{x}, \vec{x}+\alpha\omega)\,\frac{\cos\theta}{\pi}\,\mathrm{d}\omega$$où $\theta$ est l'angle entre la direction $\omega$ et la normale au point $\vec{x}$. La variable $\alpha$ permet d'ajuster la distance maximale jusqu'à laquelle l'effet d'occlusion est considérée.
4.1. Échantillonnage d'un hémisphère
Pour calculer cette intégrale au sens de Monte-Carlo, il vous faut échantillonner l'hémisphère au point $\vec{x}$ orienté selon la normale $\vec{n}$. Pour cela, vous allez compléter la classe Warp qui permet de transformer un échantillonnage uniforme du carré unité $[0,1[ \times [0,1[$ dans un autre domaine.
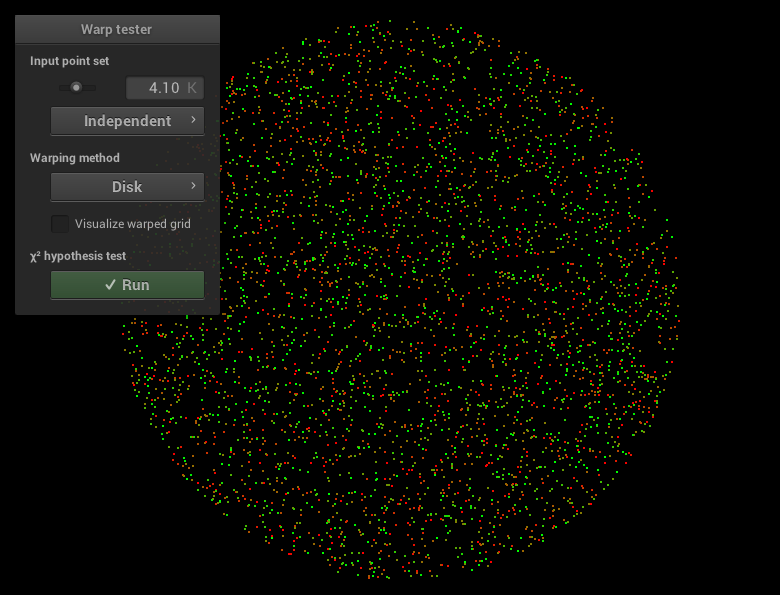
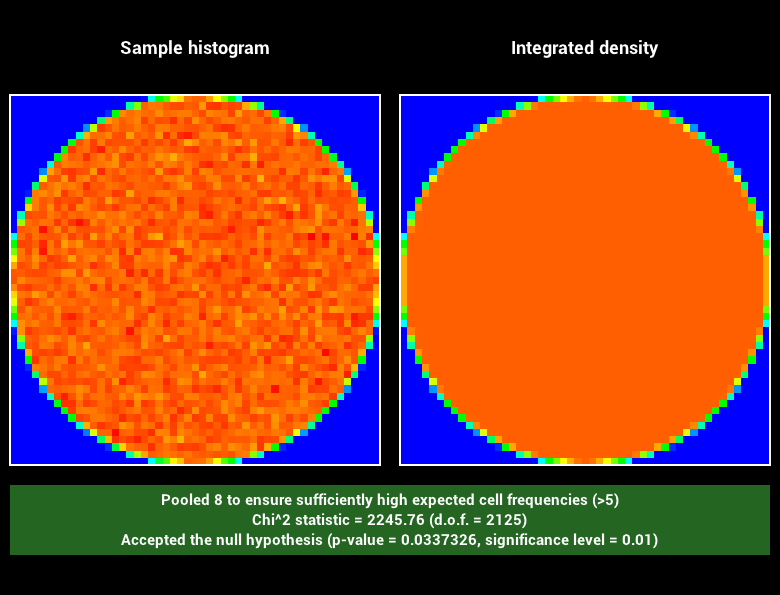
Pour vous échauffer, implémenter les fonctions Warp::squareToUniformDisk et Warp::squareToUniformDiskPdf en utilisant le cours. Pour déboguer votre code, utilisez l'utilitaire warptest qui vous permet de visualiser l'effet des fonctions de warping sur un nuage de points et de les valider par un test statistique du $\chi^2$. Vous devriez obtenir :
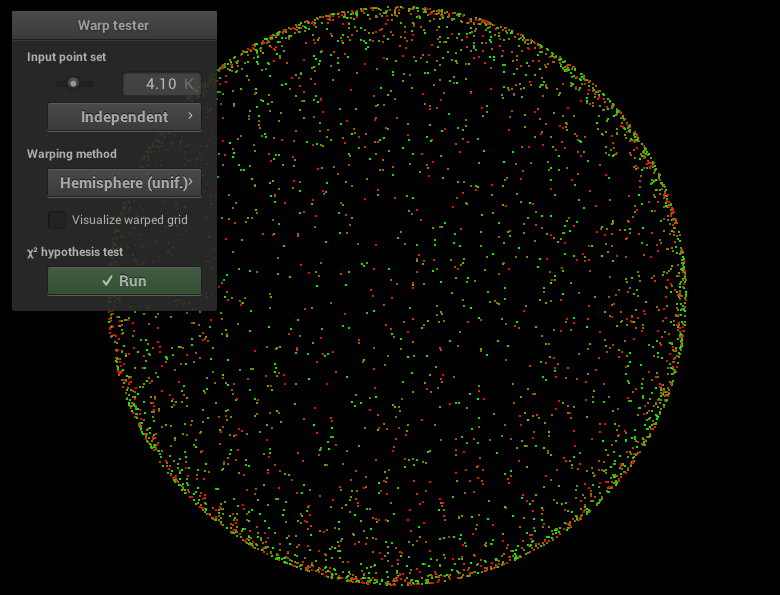
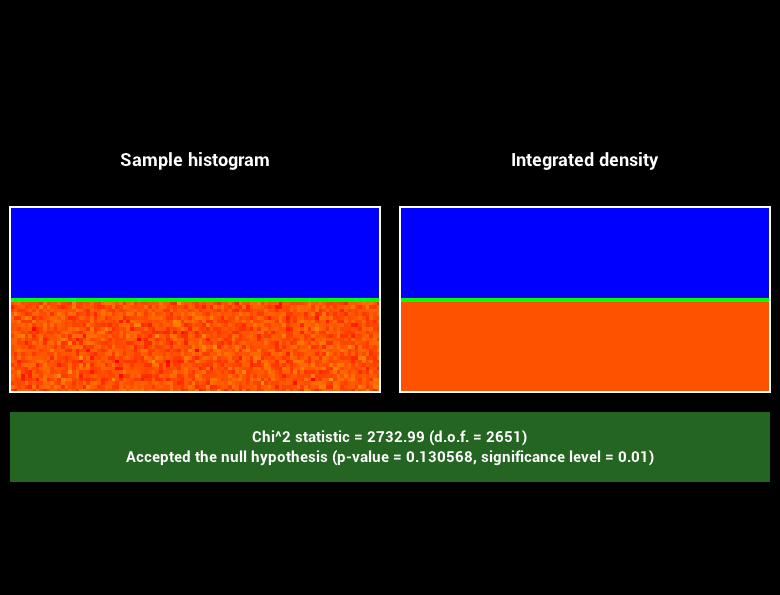
Effectuez la dérivation et implémentez ensuite la fonction Warp::squareToUniformHemisphere qui effectue la transformation vers la distribution uniforme sur l'hémisphère autour du pôle $(0,0,1)$. Complétez également Warp::squareToUniformHemispherePdf qui retourne la $pdf$ associée. Vous devriez obtenir :
Implémentez ensuite les fonctions Warp::squareToCosineHemisphere et Warp::squareToCosineHemispherePdf effectuant la transformation vers la distribution sur l'hémisphère pondérée par le cosinus (cosine-weighted hemisphere sampling).
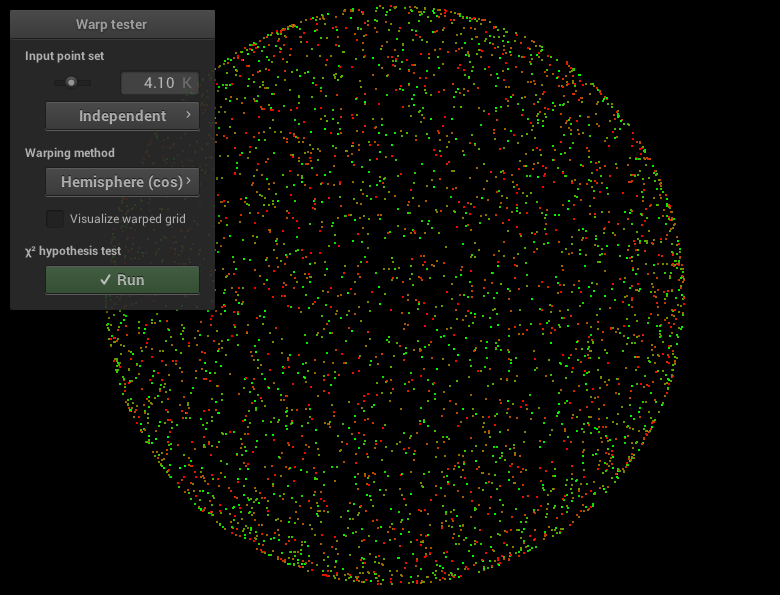
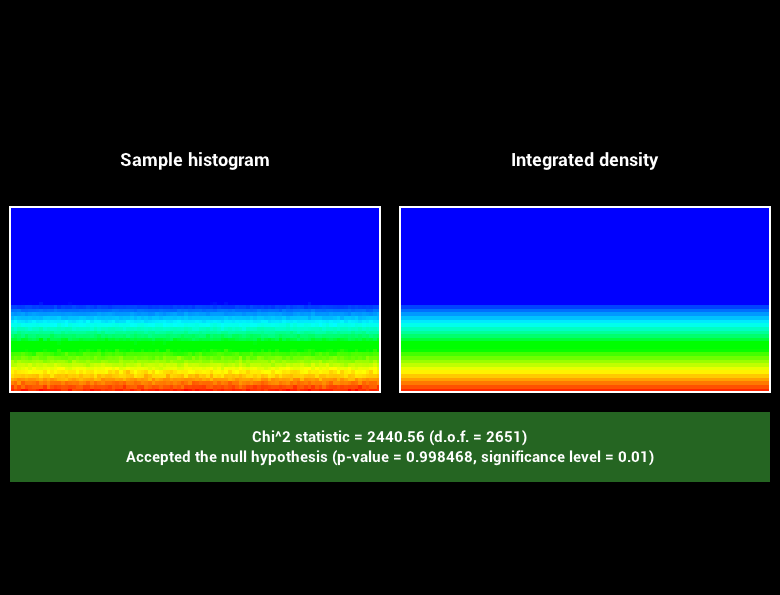
4.2. Calcul de l'AO
Complétez l'intégrateur AO évaluant la fonction de visibilité en lançant m_sampleCount rayons d'ombre dans des directions aléatoires $\vec{p}$ sur l'hémisphère. Pour cela, utilisez la fonction Warp::squareToUniformHemisphere précédente et transformez la direction aléatoire $\vec{d}$ obtenue dans l'espace local vers l'espace monde :
$$ \vec{p} = \vec{d}.x() \, \vec{u} + \vec{d}.y() \, \vec{v} + \vec{d}.z() \, \vec{n}$$
où $\vec{u}$ et $\vec{v}$ sont deux vecteurs orthogonaux dans le plan tangent à $\vec{n}$.
Moyennez les réponses de la fonction de visibilité et n'oubliez pas de pondérez par la $pdf$ adéquate. Vous pouvez faire l'hypothèse que l'occlusion est un effet global ($\alpha = \infty$). Testez également avec Warp::squareToCosineHemisphere lorsque m_cosineWeighted est à True. Vous devriez obtenir ces deux résultats pour "killeroo_ao.scn" :


Selon vous, quelle est la stratégie d'échantillonnage la plus efficace en termes de convergence et de performances ? Pourquoi ?
