Dynamic Sampling and Rendering
of Algebraic Point Set Surfaces
Eurographics 2008, Crete, Greece.
Abstract
Algebraic Point Set Surfaces (APSS) define a surface from a set of points using local moving least-squares (MLS) fitting of algebraic spheres. In this paper we first revisit the spherical fitting problem and provide a new, more generic solution that includes intuitive parameters for curvature control of the fitted spheres. As a second contribution we present a novel real-time rendering system of such surfaces using a dynamic up-sampling strategy combined with a conventional splatting algorithm for high quality rendering. Our approach also includes a new view dependent geometric error tailored to efficient and adaptive up-sampling of the surface. One of the key features of our system is its high degree of flexibility that enables us to achieve high performance even for highly dynamic data or complex models by exploiting temporal coherence at the primitive level. We also address the issue of efficient neighbor queries and discuss several spatial search data structures with respect to construction, access and GPU friendliness. Finally, we present an efficient parallel GPU implementation of the algorithms and search structures.

Smooth variation of the curvature parameter from 8 to 1 (top) and 1 to -4.5 (bottom). Note the inversion effect on the surface microstructure.
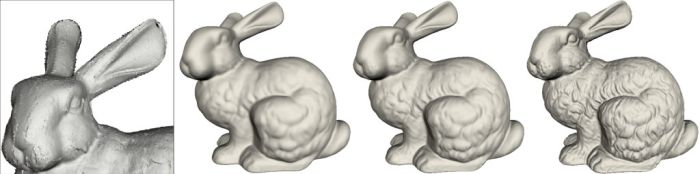
APSS reconstruction of a noisy data (left) using different values of the curvature control paramter: -1, 0.5, 5.
