The Oriented Coloring Page
This page is no longer maintained.
This page is maintained by Éric Sopena and is intended to collect results on oriented colorings that have been published in refereed journals or conferences. Some arXiv papers, yet unpublished, might also be cited, in which case the corresponding paragraphs appear in italics.
If you have any suggestion, or new result not mentioned here, please do not hesitate to contact me at eric.sopena@labri.fr.
Contents
- Definitions and notation (oriented graphs, oriented colorings, homomorphisms, oriented chromatic number, oriented cliques, oriented clique numbers)
- General results (bounds, forests, cycles, graphs with bounded acyclic chromatic number, graphs with bounded maximum average degree, critical graphs, complexity)
- Planar graphs (grids, outerplanar graphs, 2-outerplanar graphs, planar graphs, planar graphs with large girth)
- Graphs with bounded degree (general bounds, graphs with maximum degree three, graphs with larger maximum degree)
- Other graph classes (Cartesian products, Halin graphs, hypercubes, graphs with given excess, fully subdivided graphs)
- Miscellaneous (oriented arc-coloring, strong oriented colorings, pushable chromatic number, injective oriented colorings, oriented list coloring, oriented coloring game)
- References
Definitions and notation
Oriented graphs
An oriented graph is a digraph with no loops and no opposite arcs. An oriented graph is thus an orientation of a simple undirected graph U, obtained from U by giving to each edge of U one of its two possible orientations.
We denote by V(G) and A(G) the set of vertices and the set of arcs, respectively, of an oriented graph G.
Oriented colorings
An oriented k-coloring of an oriented graph G is a mapping c: V(G) → C, where C is a set of k colors (usually C = {1,...,k}), such that:
- c(u) ≠ c(v) for every arc uv in A(G),
- c(u) ≠ c(y) for every two arcs uv and xy with c(v) = c(x).
Note in particular that if uvw is a directed path in G (that is uv, vw ∈ A(G)), then c(u) ≠ c(v) ≠ c(w) ≠ c(u).
An oriented k-coloring of an oriented graph G thus corresponds to a partition of the vertex set V(G) of G into k independent subsets such that all the arcs linking any two of these subsets have the same direction.
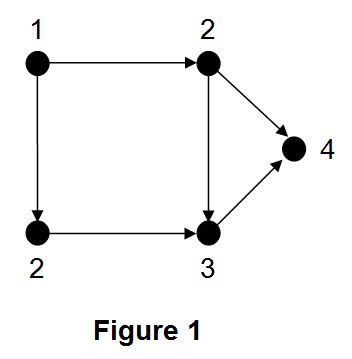
Example. Figure 1 shows an oriented 4-coloring of an oriented graph. It can be observed that this graph admits no oriented 3-coloring.
Colorings of oriented graphs first appear in the work of Courcelle (Co94) on the monadic second order logic of graphs, as a way to encode graph orientations by means of vertex labels. Since then, these colorings have been considered by many authors, following the work of Raspaud and Sopena (RS94) on oriented colorings of planar graphs (see (So01, So16) for two surveys on oriented colorings).
Homomorphisms
Let G and H be two oriented graphs. A homomorphism from G to H is a mapping h: V(G) → V(H) which preserves the arcs: uv ∈ A(G) ⇒ h(u)h(v) ∈ A(H). We write G → H whenever there exists a homomorphism from G to H.
A homomorphism from G to H can therefore be viewed as an oriented coloring of G that uses the vertices of H as colors. An oriented k-coloring of G can thus be equivalently defined as a homomorphism of G to some oriented graph H on k vertices.
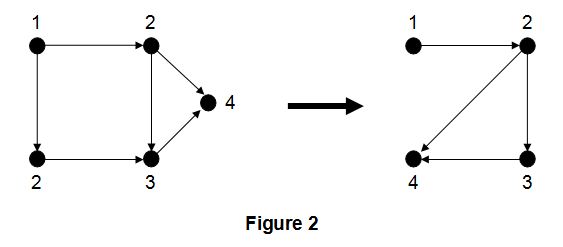
Example. Figure 2 shows how the oriented 4-coloring of Figure 1 can be interpreted as a homomorphism to an oriented graph of order 4.
Oriented chromatic number
The oriented chromatic number χo(G) of an oriented graph G is defined as the smallest k for which G admits an oriented k-coloring or, equivalently, as the smallest order of an oriented graph H such that G admits a homomorphism to H.
The oriented chromatic number χo(U) of an undirected graph U is defined as the maximum oriented chromatic number of its orientations: χo(U) = max { χo(G), G is an orientation of U }.
Examples.
- As observed above, the oriented chromatic number of the graph depicted in Figure 1 is 4.
- Let C5 be the directed cycle on 5 vertices. Since any two vertices of C5 are linked by a directed path of length at most 2, we get χo(C5) = 5.
Oriented cliques (or o-cliques)
An oriented graph G is an oriented clique (or, simply, an o-clique) if χo(G) = |V(G)|. Therefore, an oriented graph is an o-clique if and only if every two of its vertices are linked (in either direction) by a directed path of length 1 or 2 (in other words, its weak diameter is at most 2).
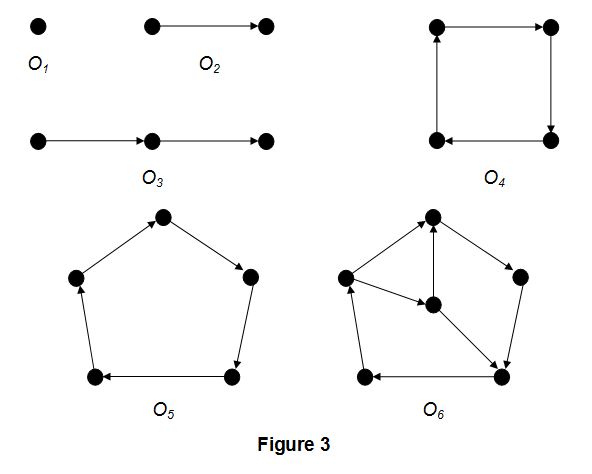
Every tournament is obviously an o-clique but being a tournament is not a necessary condition for being an o-clique. Figure 3 depicts some sample o-cliques of order up to 6.
Let On be an o-clique of order n. Take now two copies of On, a new vertex v, and add all possible arcs from vertices of the first copy towards the vertex v and all possible arcs from the vertex v to vertices of the second copy. It is easy to check that the so-obtained oriented graph is an o-clique of order 2n + 1. (The o-clique O3 in Figure 3 is obtained in this way from the o-clique O1.)
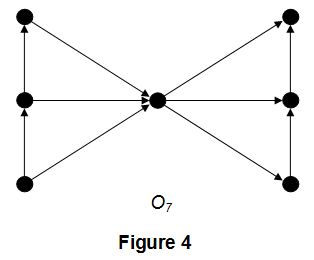
In (KMG04a), Klostermeyer and MacGillivray proved that the maximum order of an o-clique whose underlying graph is a partial 2-tree graph is 7 (which implies, in particular, that the maximum order of an outerplanar o-clique is 7; Figure 4 below shows an outerplanar o-clique of order 7). They also proved that every planar o-clique has order at most 36 and conjectured that the maximum order of a planar o-clique is 15. Observe that applying the above-described construction to the outerplanar o-clique of Figure 4 produces a planar o-clique of order 15. This conjecture has been proved by Sen in (Se12) (another proof was given later by Nandy, Sen and Sopena in (NSS16)).
In (FHPZ98) and (KLSS99), Füredi, Horak, Pareek and Zhu, and Kostochka, Łuczak, Simonyi and Sopena, respectively, independently proved that the minimum number of edges in an o-clique of order n is (1 + o(1))nlog2n.
It is not difficult to check that the maximum order of a subcubic o-clique is 7. In (DPOS20), Dybizbański, Ochem, Pinlou and Szepietowski proved that the maximum order of an o-clique with maximum degree 4 (resp. 5) is 12 (resp. lies between 16 and 18).
Oriented clique numbers
Two types of clique numbers are defined for oriented graphs. The absolute oriented clique number ωao(G) of an oriented graph G is the maximum order of an o-clique subgraph of G. The relative oriented clique number ωro(G) of an oriented graph G is the maximum cardinality of a set of vertices in G with the property that every two vertices in this set are connected by a directed path of length 1 or 2 in G (in other words, in every oriented coloring of G, all the vertices in such a set must be assigned distinct colors; such a set is called a relative oriented clique, or relative o-clique of G). It follows from these definitions that we have ωao(G) ≤ ωro(G) ≤ χo(G) for every oriented graph G.
In (NSS16), Nandy, Sen and Sopena studied the absolute oriented clique number of planar graphs with given girth. They prove that ωao(G) ≤ 15, 6, 5 or 3, if G is a planar graph with girth at least 3, 4, 5 or 6, respectively, and that all these bounds are sharp. (The fact that ωao(G) ≤ 15 for every planar graph G was already proved in (Se12).)
Relative oriented clique numbers of oriented graphs have been studied by Das, Prabhu and Sen in (DPS19). They proved the following results:
- ωro(G) ≤ 7 if G has maximum degree at most 3, and this bound is sharp,
- ωro(G) ≤ 7, 5 or 3 if G is an outerplanar graph with girth at least 3, 4 or 5, or 6, respectively, and all these bounds are sharp,
- ωro(G) ≤ 32, 14, 6, 4, 3 if G is a planar graph with girth at least 3, 4, 5, 6 or 7, respectively. Moreover, there exist planar graphs with relative oriented clique number 15, and triangle-free planar graphs with relative oriented clique number 10, while the bounds for girth 5, 6 and 7 are sharp.
They also proved that determining the relative oriented clique number of an oriented bipartite graph is an NP-hard problem.
General results
Bounds
In (OM17), Ochem and Movarraei proved that for every undirected graph G, χo(G) ≤ χ(G)χ2(G) and χ2(G) ≤ χ(G)χo(G), where χ(G) is the ordinary chromatic number of G, and χ2(G) the 2-edge-colored chromatic number of G (see (OM17) for details).
Forests
It is not difficult to observe that every oriented forest F admits a homomorphism to C3, the directed cycle of order 3, so that χo(T) ≤ 3.
Cycles
As observed above, the directed cycle on 5 vertices is an o-clique and, therefore, has oriented chromatic number 5. It is not difficult to prove that every other oriented cycle has oriented chromatic number at most 4.
More precisely, if C is an oriented cycle, we define the level λ(C) of C as the number of forward arcs minus the number of backward arcs in C. Then we have (1) if the orientation of C is alternating, then χo(C) = 2, (2) if λ(C) = 0 (mod 3) and the orientation of C is not alternating, then C admits a homomorphism to C3 and χo(C) = 3, (3) if C does not contain three consecutive arcs with the same direction and the orientation of C is not alternating, then C admits a homomorphism to T3, the transitive tournament or order 3, and χo(C) = 3, (4) otherwise, χo(C) = 4 if and only if C is not the o-clique O5 (depicted in Figure 3).
Graphs with bounded acyclic chromatic number
A proper vertex coloring of an undirected graph U is acyclic if for every two colors a and b, the subgraph of U induced by the vertices with color a or b is a forest. In others words, every cycle of U uses at least three colors. The acyclic chromatic number of U, denoted χa(U), is then the smallest number of colors needed by an acyclic coloring of U.
In (RS94), Raspaud and Sopena proved that every graph with acyclic chromatic number at most k has oriented chromatic number at most k.2k-1. (Ochem (Oc05) proved that this bound is tight for every k ≥ 3.)
Conversely, Kostochka, Sopena and Zhu proved in (KSZ97) that every class of graphs with bounded oriented chromatic number has bounded acyclic chromatic number.
Graphs with bounded maximum average degree
The maximum average degree mad(U) of an undirected graph U is defined as the maximum of the average degrees of its subgraphs (the average degree of H is given by 2.|E(H)| / |V(H)|).
Recall that the girth of U is the length of a shortest cycle in U.
If U is a planar graph with girth at least g, then, using Euler's formula, it can be proved that U has maximum degree less than 2g/(g-2). Therefore,
several authors have considered the problem of determining the oriented chromatic number of graphs with bounded maximum average degree (and, sometimes, with high girth), in order to get upper bounds on the oriented chromatic number of planar graphs with high girth:
Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99),
Borodin, Ivanova and Kostochka (BIK07),
Pinlou (Pi09).
The best known upper bounds are summarized in the table below (some of them giving the best known upper bounds for planar graphs with high girth).
| Mad | Girth | Χo | Author(s) |
|---|---|---|---|
| < 10/3 | ≤ 19 | Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99) | |
| < 10/3 | ≥ 5 | ≤ 16 | Pinlou (Pi09) |
| < 3 | ≤ 11 | Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99) | |
| < 11/4 | ≥ 5 | ≤ 7 | Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99) |
| < 12/5 | ≥ 5 | ≤ 5 | Borodin, Ivanova and Kostochka (BIK07) |
Critical graphs
An oriented graph G is vertex-critical (resp. arc-critical) if, for every vertex u in V(G) (resp. for every arc uv in A(G)), χo(G - u) < χo(G) (resp. χo(G - uv) < χo(G)).
In (BFKRS01), Borodin, Fon-der-Flaass, Kostochka, Raspaud and Sopena proved that for every k > 0, there exists an oriented graph Gk such that χo(Gk) - χo(Gk - u) ≥ k for every vertex u in V(Gk) and χo(Gk) - χo(Gk - uv) = 2 for every arc uv in A(Gk) (it is not difficult to observe that χo(G) - χo(G - uv) ≤ 2 for every oriented graph G and every arc uv in A(G)).
Complexity
In (KMG04b), Klostermeyer and MacGillivray proved the following: for a given oriented graph G, whether χo(G) ≤ k can be decided in polynomial time if k ≤ 3 and is NP-complete if k ≥ 4, even when G is connected. Culus and Demange (CD06) proved that deciding whether χo(G) ≤ 4 is NP-complete even if G is a bounded degree bipartite, or a bounded degree acyclic oriented graph. Ganian and Hliněný (GH10) proved that this problem is also NP-complete when restricted to graphs with K-width 1 and DAG-depth 3 (see (GH10) for details), and Coelho, Faria, Gravier and Klein (CFGK16) proved that this problem is stll NP-complete when restricted to acyclic oriented graphs whose underlying graph is connected, planar, bipartite and has maximum degree 3.
Ganian (Ga09) proved that there exists an FPT-algorithm for determining the oriented chromatic number of an oriented graph, parameterized by the treewidth of its underlying undirected graph.
Planar graphs
Grids
The rectangular grid Gm,n is the Cartesian product of Pm by Pn, the two paths with m and n vertices, respectively.
In (FRR03), Fertin, Raspaud and Roychowdhury proved that the oriented chromatic number of every rectangular grid is at most 11, and that there exists such grids with oriented chromatic number 7 (they provided an orientation of the grid G4,5 with oriented chromatic number 7). They also conjectured that the oriented chromatic number of every rectangular grid is at most 7, and that every such grid admits a homomorphism to the tournament T7 (see below). They proved that this conjecture is true when m = 2,3.
The tournament T7 is built from the non-zero quadratic residues of 7; it has vertex set V(T7) = Z/7Z and ij is an arc if and only if j - i ∈ {1,2,4}.
Szepietowski and Targan (ST04) proved that this conjecture is also true when m = 4 but that the second part of the conjecture fails to be true whenever m ≥ 5 by providing an orientation of G5,33 which admits no homomorphism to the tournament T7. The first part of the conjecture was finally disproved by Dybizbański and Nenca (DN12) who exhibited an orientation of the rectangular grid G7,212 with oriented chromatic number at least 8.
In (Bi06), Bielak studied hexagonal grids Hm,n, made of m rows of n hexagons. She proved that χo(H1,n) = 5 for every n ≥ 3 and that χo(Hm,n) ≤ 6 for every m, n.
Outerplanar graphs
In (So97), it was proved that every partial 2-tree has oriented chromatic number at most 7. Since every outerplanar graph is a partial 2-tree, we get that every outerplanar graph has oriented chromatic number at most 7. This bound is tight, as shown by the outerplanar o-clique O7 depicted in Figure 4.
In (PS06), Pinlou and Sopena determined the oriented chromatic number of outerplanar graphs of given girth.
They proved that every outerplanar graph (in fact, more generally, that every partial 2-tree) with girth g has oriented chromatic number at most 6 is g ≥ 4, and at most 5 if g ≥ 5. Moreover, all these bounds are tight.
2-Outerplanar graphs
A graph is 2-outerplanar if it has a planar embedding such that the subgraph obtained by removing the vertices of the external face is outerplanar. In (EO07), Esperet and Ochem proved that every 2-outerplanar graph has oriented chromatic number at most 67. This bound was later decreased to 40 by Ochem and Pinlou (OP14).
Planar graphs
In (Bo79), Borodin proved that every undirected planar graph is acyclically 5-colorable. Therefore, using the result of Raspaud and Sopena (RS94), we get that every planar graph has oriented chromatic number at most 5.24 = 80. Despite many efforts, this upper bound has not been improved yet.
As observed above, there exists a planar o-clique of order 15. This lower bound on the oriented chromatic number of the class of planar graphs has been improved to 16 by Sopena (So02), to 17 by Marshall (Ma07), and to 18, again by Marshall (Ma12).
Planar graphs with large girth
Several authors have considered the problem of determining the oriented chromatic number of the families of planar graphs with given girth, successively improving various lower or upper bounds:
Raspaud and Sopena (RS94),
Nešetřil, Raspaud and Sopena (NRS97),
Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS98, BKNRS99),
Ochem (Oc04),
Borodin, Kim, Kostochka and West (BKKW04),
Borodin and Ivanova (BI05a, BI05b),
Esperet and Ochem (EO07),
Borodin, Ivanova and Kostochka (BIK07),
Montassier, Ochem and Pinlou (MOP08),
Ochem and Pinlou (OP08, OP14),
Pinlou (Pi09),
Marshall (Ma12, Ma13).
The best known lower and upper bounds are summarized in the table below (first reference is for the lower bound, second reference for the upper bound).
| Girth | Χo | Author(s) |
|---|---|---|
| ≥ 3 | 18 ≤ Χo ≤ 80 | Marshall (Ma12) - Raspaud and Sopena (RS94) |
| ≥ 4 | 11 ≤ Χo ≤ 40 | Ochem (Oc04) - Ochem and Pinlou (OP14) |
| ≥ 5 | 7 ≤ Χo ≤ 16 | Marshall (Ma13) - Pinlou (Pi09) |
| ≥ 6 | 7 ≤ Χo ≤ 11 | Marshall (Ma13) - Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99) |
| ≥ 7 | 6 ≤ Χo ≤ 7 | Nešetřil, Raspaud and Sopena (NRS97) - Borodin and Ivanova (BI05a) |
| ≥ 8 | 5 ≤ Χo ≤ 7 | Nešetřil, Raspaud and Sopena (NRS97) - Borodin and Ivanova (BI05a) |
| ≥ 11 | 5 ≤ Χo ≤ 6 | Nešetřil, Raspaud and Sopena (NRS97) - Ochem and Pinlou (OP08) |
| ≥ 12 | Χo = 5 | Nešetřil, Raspaud and Sopena (NRS97) - Borodin, Ivanova and Kostochka (BIK07) |
In (BKKW04), Borodin, Kim, Kostochka and West proved that every oriented graph with girth at least 13 embeddable on the torus or the Klein bottle has oriented chromatic number at most 5.
Graphs with bounded degree
General bounds
It was proved in (So97) that every oriented graph with maximum degree Δ has oriented chromatic number at most (2Δ - 1).22Δ-2.
This bound was decreased to 2.Δ2.2Δ by Kostochka, Sopena and Zhu (KSZ97).
(These authors also proved that for every Δ ≥ 2, there exists an oriented graph with maximum degree Δ and oriented chromatic number at least 2Δ/2.)
This upper bound has been specialised by Aravind and Subramanian (AS09) as follows. Recall that the degeneracy of a graph G is the smallest integer d such that every subgraph of G contains a vertex of degree at most d. They proved that every graph with maximum degree Δ and degeneracy d has oriented chromatic number at most 16.Δ.d.2d.
In (Wo07), Wood proved that every oriented graph of order n with maximum degree Δ has oriented chromatic number at most 2Δ.sqrt(n - 1) and constructed such graphs with oriented chromatic number at least Δ.sqrt(n/8).
Graphs with maximum degree three
It was proved in (So97) that every oriented graph with maximum degree 3 has oriented chromatic number at most 16. This upper bound has been decreased to 11 by Sopena and Vignal (SV96). This bound was then decreased to 9 for connected graphs by Duffy, MacGillivray and Sopena in (DMGS19).
 The connectivity condition has been proved to be unnecessary by Dybizbański, Ochem, Pinlou and Szepietowski in (DPOS20). This bound has been decreased to 8 for connected graphs by Duffy in a paper available on arXiv: A note on colourings of connected oriented cubic graphs.
The connectivity condition has been proved to be unnecessary by Dybizbański, Ochem, Pinlou and Szepietowski in (DPOS20). This bound has been decreased to 8 for connected graphs by Duffy in a paper available on arXiv: A note on colourings of connected oriented cubic graphs.
The following conjecture was proposed in (So97):
Conjecture. Every connected oriented graph with maximum degree 3 has oriented chromatic number at most 7.
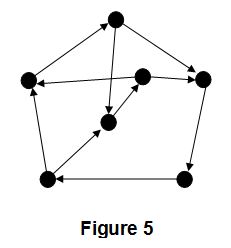
If the conjecture is true, then the bound of 7 cannot be improved, as shown by the oriented o-clique of order 7 depicted in Figure 5.
Graphs with larger maximum degree
Duffy, MacGillivray and Sopena proved in (DMGS19) that every connected oriented graph with maximum degree 4 has oriented chromatic number at most 69. In (DPOS20), Dybizbański, Ochem, Pinlou and Szepietowski decreased this bound to 26, showing again that the connectivity condition is unnecessary. They also proved that every graph with maximum degree 5, 6 or 7 has oriented chromatic number at most 90, 306 or 1322, respectively.
Other graph classes
Cartesian products
The Cartesian product of two undirected graphs U and U′, denoted U □ U′, is the graph defined by V(U □ U′) = V(U) × V(U′) and (u,u′)(v,v′) ∈ E(U □ U′) if and only if either u = u′ and vv′ ∈ E(U′) or v = v′ and uu′ ∈ E(U).
In (ANS11), Aravind, Narayanan and Subramanian proved that for every undirected graph U:
- χo(U □ Pk) ≤ (2k - 1).χo(U), for every k ≥ 2,
- χo(U □ Ck) ≤ 2k.χo(U), for every k ≥ 3,
where Pk and Ck stands for the path and the cycle on k vertices, respectively.
These results were immproved in (So12), where it is proved that χo(U □ T) ≤ 6χo(U) for every undirected tree T, χo(U □ Ck) ≤ 12χo(U) for every k ≥ 3, k ≠ 5 and χo(U □ C5) ≤ 15χo(U).
Halin graphs
A Halin graph is a planar graph which has a planar embedding such that deleting the edges of its external face gives a tree with at least three vertices. Hosseini Dolama and Sopena proved in (HDS06b) that every oriented Halin graph has oriented chromatic number at most 9 and that there exist oriented Halin graphs with oriented chromatic number at least 8. In (DS14), Dybizbański and Szepietowski finally proved that every oriented Halin graph has oriented chromatic number at most 8, and thus this bound is tight.
Hypercubes
In (Wo07), Wood proved that, for the d-dimensional hypercube Qd, 0.8007...sqrt(2d) ≤ χo(Qd) ≤ 2d.sqrt(2d - 1).
Graphs with given excess
The excess of a graph G is the minimum number of edges that must be deleted from G in order to get a forest. In (HDS06a), Hosseini Dolama and Sopena proved that every oriented graph with excess k has oriented chromatic number at most k + 3, except for graphs with excess 1 containing a directed cycle of length 5 which have oriented chromatic number 5. This bound is tight for every k ≤ 4.
Fully subdivided graphs
Let U be an undirected graph. We denote by Us the (undirected) graph obtained from U by subdividing exactly once every edge of U. Wood (Wo05) proved that for every undirected graph U, the oriented chromatic number of Us is at most 7 is Χ(U) ≤ 7, at most 9 if Χ(U) = 8 and equals Χ(U) if Χ(U) ≥ 9, where Χ(U) stands for the ordinary chromatic number of U.
Miscellaneous
Oriented arc-coloring
Let G be an oriented graph. The line-digraph of G, denoted LD(G), is the oriented graph whose set of vertices is the set of arcs of G, and whose set of arcs if the set of pairs (uv,vw) such that uv and vw are both arcs in G. An oriented k-arc-coloring of G is then defined as an oriented (vertex) k-coloring of LD(G). In other words, an oriented k-arc-coloring of G is a mapping c from A(G) to a set C of k colors such that:
- c(uv) ≠ c(vw) for every arcs uv and vw in A(G),
- if uv, vw, xy and yz are four arcs in A(G) with c(uv) = c(yz), then c(vw) ≠ c(xy).
The oriented chromatic index of G, denoted Χ′o(G), is then the smallest k such that G admits an oriented k-arc-coloring.
Let G be an oriented graph with oriented chromatic number k and γ be an oriented (vertex) k-coloring of G. It is not difficult to check that the mapping c defined by c(uv) = γ(u) for every arc uv in G is an oriented k-arc-coloring of G. Therefore, Χ′o(G) ≤ χo(G) for every oriented graph G.
The main results concerning the oriented chromatic index of oriented graphs are the following:
- If the underlying undirected graph of G has acyclic chromatic number at most k, then Χ′o(G) ≤ 2k(k - 1) - ⌊k/2⌋ - Ochem, Pinlou and Sopena, (OPS08).
- As a corollary of the above result, we get that every oriented planar graph has chromatic index at most 38; moreover, there exist oriented planar graphs with oriented chromatic index at least 10 - Ochem, Pinlou and Sopena, (OPS08).
- If G is a planar oriented graph with girth g ≥ 46, then Χ′o(G) ≤ 4 - Ochem, Pinlou and Sopena, (OPS08).
- For every partial 2-tree G, Χ′o(G) ≤ 7 and this bound is tight - Pinlou and Sopena, (PS06).
- Every outerplanar graph with girth g has oriented chromatic index at most 7 if g ≥ 3, at most 6 is g ≥ 4, at most 5 if 5 ≤ g ≤ 9 and at most 4 if g ≥ 10; moreover, all these bounds are tight - Pinlou and Sopena, (PS06).
- Every partial 2-tree with girth g has oriented chromatic index at most 7 if g ≥ 3, at most 6 is g ≥ 5, at most 5 if 7 ≤ g ≤ 17 (tight) and at most 4 if g ≥ 18 (tight) - Ochem and Pinlou, (OP07).
- If G is an oriented graph with maximum degree Δ, then Χ′o(G) ≤ 2.(⌊Δ2/2⌋ + Δ) - Ochem, Pinlou and Sopena, (OPS08).
- If G is an oriented graph with maximum degree 3, then Χ′o(G) ≤ 7, and there exists such oriented graphs with oriented chromatic index at least 6 - Pinlou (Pi06).
- Given an oriented graph G, deciding whether Χ′o(G) ≤ k is polynomial time if k ≤ 3 and NP-complete if k ≥ 4 - Ochem, Pinlou and Sopena, (OPS08).
Strong oriented coloring
Strong colorings of oriented graphs have been introduced by Nešetřil and Raspaud in (NR99).
A strong coloring of an oriented graph G is a homomorphism of G to an oriented Cayley graph X = X(M,A), where M is a group and A a subset of M such that A ∩ A-1 = ∅.
The smallest order of a group M for which there exists a subset A of M satisfying the previous conditions is the strong oriented chromatic number of G, denoted Χs(G).
Nešetřil and Raspaud proved in (NR99) that if G is an oriented graph with acyclic chromatic number k, then Χs(G) ≤ 6k. Thanks to Borodin's Theorem (Bo79), this yields that every oriented planar graph has strong oriented chromatic number at most 7776. This upper bound has then be decreased to 672 by Šamál (Sa03) and to 271 by Marshall (Ma06).
In (Sa04), Šamál proved that every oriented graph with oriented chromatic number at most q has strong oriented chromatic number at most (1 + o(1))).q2 and that this bound is tight.
(He also proved that every oriented graph with acyclic chromatic number at most k has strong oriented chromatic number at most 64/49.k2.2k which, for planar graphs, gives an upper bound of 1045 for the strong oriented chromatic number.)
Nešetřil and Raspaud (NR99) also considered planar graphs with large girth. They proved that if G is an oriented planar graph with girth at least g then Χs(G) is at most 5 if g ≥ 14, at most 7 if g ≥ 8, at most 11 if g ≥ 6 and at most 19 if g ≥ 5.
Several results about upper bounds on the oriented chromatic number of certain graph classes were obtained by proving that every member of the class admits a homomorphism to some oriented graph which is indeed a Cayley graph, so that these results also hold for the strong oriented chromatic number. Hence we get for instance:
- if G is an oriented outerplanar graph (or, more generally, an oriented partial 2-tree), then Χs(G) ≤ 7, Sopena (So97),
- if G is an oriented 2-outerplanar graph, then Χs(G) ≤ 67, Esperet and Ochem (EO07),
- if G is an oriented graph with maximum average degree less than 10/3 (resp. 3, 11/4), then Χs(G) ≤ 19 (resp. 11, 7), Borodin, Kostochka, Nešetřil, Raspaud and Sopena (BKNRS99),
- if G is an oriented rectangular grid, then Χs(G) ≤ 11, Fertin, Raspaud and Roychowdhury (FRR03),
- if G is a graph with maximum degree 3, then Χs(G) ≤ 11, Sopena and Vignal (SV96).
Pushable chromatic number
Klostermeyer and MacGillivray introduced in (KMG04b) (see also (KMG04c)) the notion of the pushable chromatic number of an oriented graph G. If Y is a subset of V(G), we denote by GY the oriented graph obtained from G by reversing the orientation of all the arcs that have exactly one end in Y. The pushable chromatic number of G, denoted Χp(G), is then defined as the minimum oriented chromatic number of the oriented graphs GY, taken over all possible subsets Y of V(G).
It is not difficult to observe that Χp(G) ≤ χo(G) ≤ 2.Χp(G) for every oriented graph G. Klostermeyer and MacGillivray proved that every oriented partial 2-tree has pushable chromatic number at most 4. Moreover, they proved that the problem of deciding if an oriented graph has pushable chromatic number at most k is polynomial if k ≤ 2 and NP-complete if k ≥ 3.
A push-clique is an oriented graph whose pushable chromatic number equals its order. In (BNS17), Bensmail, Nandi and Sen proved that deciding whether an undirected graph can be oriented in such a way that the resulting oriented graph is a push-clique is an NP-complete problem. Moreover, they proved that the maximum order of a planar push-clique is 8 (and this bound is sharp), and characterized all planar push-cliques in terms of spanning subraphs (see (BNS17) for details).
Injective oriented colorings
Oriented colorings that are injective on in-neighborhoods first appeared in the work of Courcelle (Co94), under the name of good and semi-strong colorings. An oriented k-coloring is said to be injective if, for every vertex u in V(G), all the in-neighbors of u are assigned distinct colors. It follows from Courcelle's Theorem on the monadic second order logic of graphs that deciding, for a fixed number k of colors, if an oriented graph G admits an injective oriented k-coloring is polynomially solvable if G has bounded treewidth.
In (RS94), Raspaud and Sopena proved that every oriented planar graph admits an injective oriented 320-coloring.
The interest in injective oriented colorings has been reactivated by MacGillivray, Raspaud and Swarts with their WG'09 paper (MGRS10).
Injective oriented colorings may obviously be interpreted in terms of (locally) injective homomorphisms of oriented graphs, that is arc-preserving vertex mappings such that in-neighbors are mapped to distinct vertices. In (MGS10), MacGillivray and Swarts proved that if T is a tournament, the injective T-coloring problem is NP-complete, except when T has at most three vertices or consists of a directed 3-cycle dominated by a source vertex. Moreover, the problem of deciding if an oriented connected graph admits an injective oriented k-coloring is polynomial if k ≤ 3 and NP-complete if k ≥ 4 (MGRS10). If T is an oriented tree, there exists a linear time algorithm to determine if T admits an injective oriented k-coloring, for every given fixed k (MGRS10).
In (MGRS11), MacGillivray, Raspaud and Swarts exhibited sets of forbidden subgraphs for an oriented graph to admit an injective oriented 2- or 3-coloring and described efficient algorithms that either produce such colorings or a forbidden
structure.
An io-clique is an oriented graph G that admits no injective oriented k-coloring if k < |V(G)|. (Observe that every oriented graph admits an injective oriented k-coloring with k = |V(G)|.)
MacGillivray, Raspaud and Swarts proved that G is an io-clique if and only if every two vertices in G have a common out-neighbor or are joined by a directed path of length at most 2 (MGRS10).
Let G be an oriented graph and let Δ- (resp. Δ+) denote the maximum in-degree (resp. out-degree) of G. Then G admits an injective oriented k-colouring with k ≤ 2p - 1, p = Δ+(Δ--1)Δ++(Δ+)2 (with k ≤ 2.Δ- + 1 if G is an oriented tree and, in that case, this bound is tight) (MGRS10).
Oriented list coloring
Sali and Simonyi introduced in (SS99) the notion of oriented list coloring.
An oriented graph G is k-choosable if, for every possible assignment of lists of size at least k to its vertices, there is an oriented coloring of G such that every vertex is assigned one of the colors of its list. The minimum k for which G is k-choosable is the oriented choice number of G, denoted cho(G).
If U is an undirected graph, the oriented choice number cho(U) of U is defined as the minimum oriented choice number of its orientations. (Note that this is in contrast to the oriented chromatic number of U, defined has the maximum oriented chromatic number of its orientations.)
Sali and Simonyi proved the following:
- For every k > 0, there is an integer g(k) such that, if an undirected graph U contains at least g(k) independent edges, then cho(U) > k. (As a corollary, we get that for every k > 0, there exists an undirected graph with (ordinary) choice number 2 and oriented choice number greater than k.)
- For every undirected graph U, cho(U) ≤ τ(U) + 1, where τ(U) denotes the minimum number of vertices covering all edges of U.
In (TV01), Tuza and Voigt characterized matchings, connected graphs, and graphs containing at least one cycle, with oriented choice number 2. In particular, they proved that the smallest number of edges in a matching with oriented choice number 3 is 12.
Oriented coloring game
Nešetřil and Sopena introduced in (NS01) the oriented version of the graph coloring game. Let H be any fixed oriented graph. The oriented H-coloring game is played on an oriented graph G by two players, Alice and Bob, who alternate in turn, Alice having the first move. Each move consists in choosing an uncolored vertex u in G and assigning it a color α from V(H) such that:
- if uv (resp. vu) is an arc in A(G) and v has color β, then αβ (resp. βα) is an arc in A(H),
- if there exists a directed 2-path from u to some vertex w with color γ, then α ≠ γ.
Alice's goal is to eventually produce a H-coloring of G (that is, a homomorphism from G to H) while Bob tries to prevent her from doing so. The oriented game chromatic number of G, denoted ogcn(G), is defined as the smallest k for which there exists an oriented graph H of order k such that Alice has a winning strategy when playing the oriented H-coloring game on G.
The authors proved the following:
if P is an oriented path, then ogcn(P) ≤ 7 (and this bound is tight),
if T is an oriented tree, then ogcn(T) ≤ 19,
the oriented game chromatic number of the class of oriented outerplanar graphs is finite.
In (KT01), Kierstead and Trotter proved that for every k, there exists an integer t and a tournament T of order t such that, if Γ is a topologically closed class of graphs (that is, every subgraph or subdivision of a member of Γ belongs to Γ) and Γ does not contain the complete graph Kk, then Alice wins the oriented T-coloring game on every orientation of any member of Γ. In particular, this proves that the oriented game chromatic number of the class of oriented planar graphs is finite (this question was posed in (NS01)).
In (KT03), Kierstead and Tuza proved that for every k, the oriented game chromatic number of the class of oriented partial k-trees is finite.
References
- [AS09] N.R. Aravind and C.R. Subramanian. Forbidden subgraph colorings and the oriented chromatic number. In Proc. 20th International Workshop on Combinatorial Algorithms, IWOCA'09. Lecture Notes in Comput. Sci. 5874:60-71 (2009), doi:10.1007/978-3-642-10217-2_9.
- [ANS11] N.R. Aravind, N. Narayanan and C.R. Subramanian. Oriented colouring of some graph products. Discuss. Math. Graph Theory 31(4):675-686 (2011), doi:10.7151/dmgt.1572.
- [BNS17] J. Bensmail, S. Nandi and S. Sen. On oriented cliques with respect to push operation. Discrete Appl. Math. 232:50–63 (2017). doi:10.1016/j.dam.2017.07.037. (Erratum Discrete Appl. Math. 258:276–278 (2019), doi:10.1016/j.dam.2018.09.014)
- [Bi06] H. Bielak. The oriented chromatic number of some grids. Annales UMCS Informatica AI 5:5-17 (2006).
- [Bo79]] O.V. Borodin. On acyclic colorings of planar graphs. Discrete Math. 25:211-236 (1979), doi:10.1016/0012-365X(79)90077-3.
- [BFKRS01] O.V. Borodin, D. Fon-der-Flaass, A.V. Kostochka, A. Raspaud and E. Sopena. On deeply critical oriented graphs. J. Combin. Theory, Ser. B. 81:150-155 (2001), doi:10.1006/jctb.2000.1984.
- [BI05a] O.V. Borodin and A.O. Ivanova. An oriented 7-colouring of planar graphs with girth at least 7. Sib. Electron. Math. Reports 2:222–229 (2005).
- [BI05b] O.V. Borodin and A.O. Ivanova. An oriented colouring of planar graphs with girth at least 4. Sib. Electron. Math. Reports 2:239–249 (2005).
- [BIK07] O.V. Borodin, A.O. Ivanova and A.V. Kostochka. Oriented 5-coloring of sparse plane graphs. J. Applied and Industrial Math. 1(1):9–17 (2007).
- [BKKW04] O.V. Borodin, S.J. Kim, A.V. Kostochka and D.B. West. Homomorphisms from sparse graphs with large girth. J. Combin. Theory, Ser. B. 90:147-159 (2004), doi:10.1016/S0095-8956(03)00081-9.
- [BKNRS98] O.V. Borodin, A.V. Kostochka, J. Nešetřil, A. Raspaud and E. Sopena. On universal graphs for planar oriented graphs of a given girth. Discrete Math. 188:73-85 (1998), doi:10.1016/S0012-365X(97)00276-8.
- [BKNRS99] O.V. Borodin, A.V. Kostochka, J. Nešetřil, A. Raspaud and E. Sopena. On the maximum average degree and the oriented chromatic number of a graph. Discrete Math. 206:77-89 (1999), doi:10.1016/S0012-365X(98)00393-8.
- [CFGK16] H. Coelho, L. Faria, S. Gravier and S. Klein. Oriented coloring in planar, bipartite, bounded degree 3 acyclic oriented graphs. Discrete Appl. Math. 198:109–117 (2016). doi:10.1016/j.dam.2015.06.023
- [Co94] B. Courcelle. The monadic second order logic of graphs VI: On several representations of graphs by relational structures. Discrete Appl. Math. 54:117–149 (1994), doi:10.1016/0166-218X(94)90019-1. (Erratum Discrete Appl. Math. 63:199–200 (1995), doi:10.1016/0166-218X(95)00006-D.)
- [CD06] J.-F. Culus and M. Demange. Oriented coloring: complexity and approximation. In Proc. 32nd International Conference on Current Trends in Theory and Practice of Computer Science, SOFSEM'2006. Lecture Notes in Comput. Sci. 3831:226-236 (2006), doi:10.1007/11611257_20.
- [DPS18] S. Das, S. Prabhu and S. Sen. A study on oriented relative clique number. Discrete Math. 341:2049–2057 (2018). doi:10.1016/j.disc.2018.04.001
- [DMGS19] C. Duffy, G. MacGillivray, and É. Sopena. Oriented colourings of graphs with maximum degree three and four. Discrete Mathematics 342(4):959–974 (2019). doi:10.1016/j.disc.2018.10.008
- [DN12] J. Dybizbański and A. Nenca. Oriented chromatic number of grids is greater than 7. Inform. Proc. Letters 112:113-117 (2012), 10.1016/j.ipl.2011.10.019.
- [DPOS20] Dybizbański, Ochem, Pinlou and Szepietowski. Oriented cliques and colorings of graphs with low maximum degree. Discrete Math. 343(5):111829 (2020), 10.1016/j.disc.2020.111829.
- [DS14] J. Dybizbański and A. Szepietowski. The oriented chromatic number of Halin graphs. Inform. Proc. Letters 114(1-2):45-49 (2014), 10.1016/j.ipl.2013.09.011.
- [EO07] L. Esperet and P. Ochem. Oriented colorings of 2-outerplanar graphs. Inform. Proc. Letters 101:215-219 (2007), 10.1016/j.ipl.2006.09.007.
- [FRR03] G. Fertin, A. Raspaud and A. Roychowdhury. On the oriented chromatic number of grids. Inform. Proc. Letters 85:261-266 (2003), 10.1016/S0020-0190(02)00405-2.
- [FHPZ98] Z. Füredi, P. Horak, C.M. Pareek, and X. Zhu. Minimal oriented graphs of diameter 2. Graphs Combin. 14:345–350 (1998). doi:10.1007/PL00021182
- [Ga09] R. Ganian. The Parameterized Complexity of Oriented Colouring. MEMICS 2009. Available here.
- [GH10] R. Ganian and P. Hliněný. New results on the complexity of oriented colouring on restricted digraph classes. In Proc. 36th International Conference on Current Trends in Theory and Practice of Computer Science, SOFSEM'2010. Lecture Notes in Comput. Sci. 5901:428-439 (2010), 10.1007/978-3-642-11266-9_36.
- [HDS06a] M. Hosseini Dolama and E. Sopena. On the oriented chromatic number of graphs with given excess. Discrete Math. 306(13):1342-1350 (2006), doi:10.1016/j.disc.2005.12.023.
- [HDS06b] M. Hosseini Dolama and E. Sopena. On the oriented chromatic number of Halin graphs. Inform. Proc. Letters 98(6):247-252 (2006), doi:10.1016/j.ipl.2005.03.016.
- [KT01] H.A. Kierstead and W.T. Trotter. Competitive colorings of oriented graphs. Electron. J. Combin. 8(2) (2001), paper #12.
- [KT03] H.A. Kierstead and Zs. Tuza. Marking games and the oriented game chromatic number of partial k-trees. Graphs Combin. 19(1):121–129 (2003), doi:10.1007/s00373-002-0489-5.
- [KMG04a] W.F. Klostermeyer and G. MacGillivray. Analogues of cliques for oriented coloring. Discuss. Math. Graph Theory 24:373-387 (2004), doi:10.7151/dmgt.1237.
- [KMG04b] W.F. Klostermeyer and G. MacGillivray. Homomorphisms and oriented colorings of equivalence classes of oriented graphs. Discrete Math. 274:161-172 (2004), doi:10.1016/S0012-365X(03)00086-4.
- [KMG04c] W.F. Klostermeyer and G. MacGillivray. Pushing Vertices and Oriented Colorings. Bull. Inst. Combin. Appl. 40 (2004), 49-58.
- [KLSS99] A.V. Kostochka, T. Łuczak, G. Simonyi and E. Sopena. On the minimum number of edges giving maximum oriented chromatic number. Dimacs/Dimatia conference « Contemporary Trends in Discrete Mathematics », Stirin, Czech Rep., May 1997, Dimacs Series in Discrete Math. and Theoret. Comput. Sci. 49:179-182 (1999).
- [KSZ97] A.V. Kostochka, E. Sopena and X. Zhu. Acyclic and oriented chromatic numbers of graphs. J. Graph Theory 24(4):331-340 (1997), doi:10.1002/(SICI)1097-0118(199704)24:4<331::AID-JGT5>3.3.CO;2-8.
- [MGRS10] G. MacGillivray, A. Raspaud and J. Swarts. Injective Oriented Colourings. Proc. 35th Int. Workshop on Graph-Theoretic Concepts in Computer Science, WG 2009, Lecture Notes in Comput. Sci. 5911:262-272 (2010), doi:10.1007/978-3-642-11409-0_23.
- [MGRS11] G. MacGillivray, A. Raspaud and J. Swarts. Obstructions to injective oriented colorings. Electron. Notes Discrete Math. 38:597-605 (2011), doi:10.1016/j.endm.2011.10.001.
- [MGS10] G. MacGillivray and J. Swarts. The complexity of locally injective homomorphisms. Discrete Math. 310:2685-2696 (2010), doi:10.1016/j.disc.2010.03.034.
- [Ma06] T.H. Marshall. Antisymmetric flows on planar graphs. J. Graph Theory 52(3):200-210 (2006), doi:10.1002/jgt.20154.
- [Ma07] T.H. Marshall. Homomorphism bounds for oriented planar graphs. J. Graph Theory 55:175–190 (2007), doi:10.1002/jgt.20233.
- [Ma12] T.H. Marshall. On oriented graphs with certain extension properties. Ars Combinatoria (2012), in press.
- [Ma13] T.H. Marshall. Homomorphism bounds for oriented planar graphs of given minimum girth. Graphs and Combin. 29:1489-1499 (2013), doi:10.1007/s00373-012-1202-y.
- [MOP08] M. Montassier, P. Ochem and A. Pinlou. Strong oriented chromatic number of planar graphs without short cycles. Discrete Math. Theoret. Comput. Sci. 10(1):1-24 (2008), available on line.
- [NSS16] A. Nandy, S. Sen and É. Sopena. Outerplanar and planar oriented cliques. J. Graph Theory 82(2):165–193 (2016). doi:10.1002/jgt.21893
- [NR99] J. Nešetřil and A. Raspaud. Antisymmetric flows and strong colorings of oriented graphs. Ann. Inst. Fourier 49(3):1037–1056 (1999).
- [NRS97] J. Nešetřil, A. Raspaud and E. Sopena. Colorings and girth of oriented planar graphs. Discrete Math. 165-166:519-530 (1997), doi:10.1016/S0012-365X(96)00198-7.
- [NS01] J. Nešetřil and E. Sopena. On the oriented game chromatic number. Electron. J. Combin. 8(2) (2001), paper #14.
- [Oc04] P. Ochem. Oriented colorings of triangle-free planar graphs. Inform. Proc. Letters 92:71-76 (2004), doi:10.1016/j.ipl.2004.06.012.
- [Oc05] P. Ochem. Negative results on acyclic improper colorings. Discrete Math. Theoret. Comput. Sci. Proc AE, 357-362 (2005), available here.
- [OM17] P. Ochem and N. Movarraei. Oriented, 2-edge-colored, and 2-vertex-colored homomorphisms. Inform. Proc. Lett. 123:42-46 (2017). doi:10.1016/j.ipl.2017.02.009
- [OP07] P. Ochem and A. Pinlou. Oriented vertex and arc colorings of partial 2-trees. Electron. Notes Discrete Math. 29:195-199 (2007), doi:10.1016/j.ipl.2006.06.012.
- [OP08] P. Ochem and A. Pinlou. Oriented colorings of partial 2-trees. Inform. Process. Lett. 108(2):82–86 (2008), doi:10.1016/j.ipl.2008.04.007.
- [OP14] P. Ochem and A. Pinlou. Oriented coloring of triangle-free planar graphs and 2-outerplanar graphs. Graphs and Combinatorics 30:439-453 (2014), doi:10.1007/s00373-013-1283-2.
- [OPS08] P. Ochem, A. Pinlou and E. Sopena. On the oriented chromatic index of oriented graphs. J. Graph Theory 57(4):313-332 (2008), doi:10.1002/jgt.20286.
- [Pi06] A. Pinlou. On oriented arc-coloring of subcubic graphs. Electron. J. Combin., 13:R69 (2006), available here.
- [Pi09] A. Pinlou. An oriented coloring of planar graphs with girth at least five. Discrete Math. 309:2108-2118 (2009), doi:10.1016/j.disc.2008.04.030.
- [PS06] A. Pinlou and E. Sopena. Oriented vertex and arc colorings of outerplanar graphs. Inform. Proc. Letters 100(3):97-104 (2006), doi:10.1016/j.ipl.2006.06.012.
- [RS94] A. Raspaud and E. Sopena. Good and semi-strong colorings of oriented planar graphs. Inform. Proc. Letters 51:171-174 (1994), doi:10.1016/0020-0190(94)00088-3.
- [SS99] A. Sali and G. Simonyi. Oriented list colouring of undirected graphs. Dimacs/Dimatia conference « Contemporary Trends in Discrete Mathematics », Stirin, Czech Rep., May 1997, Dimacs Series in Discrete Math. and Theoret. Comput. Sci. 49:307-316 (1999).
- [Sa03] R. Šamál. Antisymmetric flows and strong oriented coloring of planar graphs. Discrete Math. 273:203-209 (2003), doi:10.1016/S0012-365X(03)00238-3.
- [Sa04] R. Šamál. Antiflows, oriented and strong oriented colorings of graphs. Archivum Mathematicum 40:335-343 (2004), available on line.
- [Se12] S. Sen. The maximum order of a planar o-clique is 15. In Proc. 23rd International Workshop on Combinatorial Algorithms, IWOCA'12, Lecture Notes in Comput. Sci. 7643:130-142 (2012), available on line.
- [So97] E. Sopena. The chromatic number of oriented graphs. J. Graph Theory 25:191-205 (1997), doi:10.1002/(SICI)1097-0118(199707)25:3<191::AID-JGT3>3.0.CO;2-G.
- [So01] E. Sopena. Oriented graph coloring. Discrete Math. 229(1-3):359-369 (2001), doi:10.1016/S0012-365X(00)00216-8.
- [So02] E. Sopena. There exist oriented planar graphs with oriented chromatic number at least sixteen. Inform. Proc. Letters 81(6):309-312 (2002), doi:10.1016/S0020-0190(01)00246-0.
- [So12] E. Sopena. Upper oriented chromatic number of undirected graphs and oriented colorings of product graphs. Discuss. Math. Graph Theory 32(3):317-333 (2012), doi:10.7151/dmgt.1624.
- [So16] E. Sopena. Homomorphisms and colourings of oriented graphs: An updated survey. Discrete Math. 339:1993-2005 (2016), 10.1016/j.disc.2015.03.018.
- [SV96] E. Sopena and L. Vignal. A note on the oriented chromatic number of graphs with maximum degree three. Research Report (1996), available here.
- [ST04] A. Szepietowski and M. Targan. A note on the oriented chromatic number of grids. Inform. Proc. Letters 92:65-70 (2004), doi:10.1016/j.ipl.2004.06.014.
- [TV01] Zs. Tuza and M. Voigt. Oriented list colorings of graphs. J. Graph Theory 36(4):217-229 (2001), doi:10.1002/1097-0118(200104)36:4<217::AID-JGT1007>3.0.CO;2-1.
- [Wo05] D.R. Wood. Acyclic, star and oriented colourings of graph subdivisions. Discrete Math. Theoret. Comput. Sci. 7:37-50 (2005), available on line.
- [Wo07] D.R. Wood. On the oriented chromatic number of dense graphs. Contrib. Discrete Math. 2(2):145-152 (2007), available on line.