Interpolatory Refinement for Real-Time Processing of Point-Based Geometry
Eurographics 2005, Dublin, Ireland.
[bibtex] [pdf] [video1] [video2] [video3]
Abstract
The point set is a flexible surface representation suitable for both geometry processing and real-time rendering. In most applications, the control of the point cloud density is crucial and being able to refine a set of points appears to be essential. In this work, we propose a new interpolatory refinement framework for point-based geometry. First we carefully select an appropriate one-ring neighborhood around the central interpolated point. Then new points are locally inserted where the density is too low using a sqrt(3)-like refinement procedure and they are displaced on the corresponding curved Point Normal triangle. Thus, a smooth surface is reconstructed by combining the smoothing property produced by the rotational effect of sqrt(3)-like refinements with the points/normal interpolation of PN triangles. In addition we show how to handle sharp features and how our algorithm naturally fills large holes in the geometry. Finally, we illustrate the robustness of our approach, its real-time capabilities and the smoothness of the reconstructed surface on a large set of input models, including irregular and sparse point clouds.
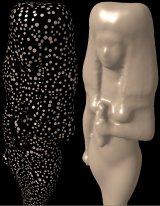



Illustration of the smooth reconstruction capabilities of our refinement procedure on the Isis model irregularly sampled with 3500 points (left). The right images focus on a particularly under-sampled area.

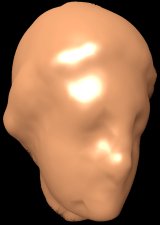
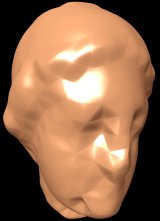

Illustration of the limitation of the PN triangle interpolation method. (click to enlarge and see per image comments)




The Igea model uniformly sampled by 600 points is refined to 150k points with various techniques. From left to right: the butterfly (after a meshing step), our diadic refinement and our new sqrt(3)-like refinement. [video2]


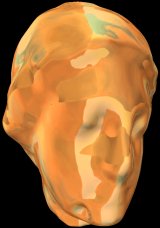
Illustration of the fractal behavior of the sqrt(3) refinement scheme (a random color is assigned to each point of the initial 600 points models and at each refinement step the color of new points is taken from the current refined point) and two environement maps applied on the refined Igea model. [video3]
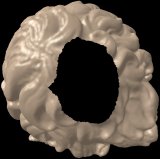
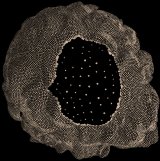


A large hole in the David's hair is filled by adjusting the radius of boundary points such that they are greater than the hole and applying our refinement algorithm. The final image is obtained after eight refinement steps while the two others show intermediate steps.
