| > | restart: |
Quasi-triangulations, weighted by their Potts polynomial, divided by q.
Catalytic variables catalytiques : x for internal digons, y for the degree of the root face
Edges t, non-root vertices w, non-root- faces z.
nu for monochromatic edges, q for the number of colours
| > |
| > |
| > |
Denote Q1(x)=coeff(Q(x,y),y,1), Q2(x)=coeff(Q(x,y),y,2)
| > | eqQ:=-Q(x,y)+1+z*t/y*(Q(x,y)-1-y*Q1(x))+q*y^2*w*t*Q(x,y)*Q(0,y) +x*y*z*t*Q1(x)*Q(x,y)+x*z*t*(Q(x,y)-1) +(nu-1)*(y*z*t*Q(x,y)*(2*x*Q1(x)+Q2(x)) +y^2*w*t/(1-x*nu*z*t)*Q(0,y)*Q(x,y) +w*t*y/(1-x*nu*z*t)/x*(Q(x,y)-Q(0,y)) ); |
![]()
![]()
| > |
| > |
| > |
Series expansion of Q
| > | Qser:=proc(n) option remember: if n=0 then 1 else convert(factor(series(subs(Q(x,y)=Qser(n-1), Q(0,y)=subs(x=0,Qser(n-1)), Q1(x)=coeff(Qser(n-1),y,1),Q2(x)=coeff(Qser(n-1),y,2), eqQ+Q(x,y)),t,n+1)),polynom): fi: end: |
| > | Qser(2); |
![]()
The coefficient of t is (q+nu-1)y ^2 w t for the isthmus
| > |
| > |
If we weight instead by the Tutte polynomial. The case of spanning trees
| > |
| > |
| > |
Connection between Q1 and Q2 : perform an expansion in y
| > | factor(subs(Q(x,0)=1,D[2](Q)(x,0)=Q1(x),Q(0,0)=1,D[2,2](Q)(x,0)=2*Q2(x),series(eqQ,y,3))); |
![]()
| > | Q1sol:=solve(coeff(%,y,1),Q1(x)); |
![]()
| > | Q2sol:=solve(coeff(%%,y,1),Q2(x)); |
![]()
From now on, z=w=1
| > | eqQ:=subs(z=1,w=1,eqQ); |
![]()
![]()
| > | Q1sol:=subs(z=1,w=1,Q1sol); Q2sol:=subs(z=1,w=1,Q2sol); |
![]()
![]()
The kernel
| > | Ker:=map(factor,collect(-coeff(eqQ,Q(x,y),1),[Q,Q1,Q2])); |
![]()
The right-hand side
| > | R:=collect(coeff(eqQ,Q(x,y),0),[Q,Q1]); |
![]()
replace Q2 by its expression in terms of Q1
| > | Ker1:=map(factor,collect(subs(Q2(x)=Q2sol,Ker),[Q,Q1])); |
![]()
| > |
Let us look for series Y(t) that cancel the kernel
| > | subs(t=0,numer(Ker)); |
![]()
To find a second series, set x=t*s
| > | subs(x=t*s,Ker); |
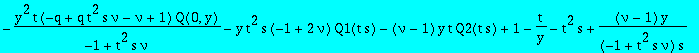
| > | factor(subs(t=0,(%*y))); |
![]()
| > |
Expansion of the séeries Y_i
| > | n:=6:res:=subs(x=t*s,subs(Q(0,y)=subs(x=0,Qser(n)), Q1(x)=coeff(Qser(n),y,1),Q2(x)=coeff(Qser(n),y,2),w=1,z=1,numer(Ker))): |
| > | with(gfun): |
| > | algeqtoseries(res,t,y,2,true); |
![[series(s/(nu-1)+(-(nu^3-3*nu^2+3*nu-1+s^3*q+s^3*nu-s^3)/(nu-1)^3)*t+O(t^2),t,2), series(1*t+(nu-1)/s*t^2+O(t^3),t,3)]](images/Potts-triang-paper22.gif)
| > |
Invariants (Section 7)
| > |
First invariant
| > | I1:=t*y*Q(0,y)*q-1/y+t/y^2; |
![]()
The second one is C^(m/2) T_m(xsubs) with
| > | CC:=t^2*q*(1+beta)^2*II^2+beta*(4*beta+q)*t*II+q*beta*(1+beta)*(q-4)*t^3+beta^2; |
![]()
| > | subs(beta=-1,%); |
![]()
| > | xsubs:=1/2*(-q+q*(1+beta)+t*q*(1+beta)*II-2*beta)/C^(1/2)-1/2*t*(q-4)*beta/C^(1/2)/y; |
![]()
| > |
| > |
The case q=1 (m=3,k=1) (Section 11.1)
| > |
| > |
| > |
Some minor calculations in Section 11 (Lemmas 19 and 20)
| > |
| > |
The case q=2 (m=4,k=1) (Section 12.2)
| > |
| > |
The case q=3 (m=6,k=1) (Section 13.2)
| > |
| > |
| > |
Back to Tutte's original equation (Section 14.2)