- -
- Le nombre d'épreuves pour obtenir
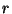 succès est une variable aléatoire
succès est une variable aléatoire 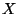 . La loi
de probabilité de cette variable aléatoire est par définition la
loi binomiale négative
. La loi
de probabilité de cette variable aléatoire est par définition la
loi binomiale négative 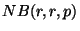 .
.
- -
- Si
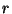 est un entier strictement positif,
est un entier strictement positif, 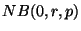 est la loi du nombre
d'échecs avant d'avoir
est la loi du nombre
d'échecs avant d'avoir 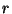
- -
- pour
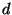 quelconque, on note la loi binomiale négative
quelconque, on note la loi binomiale négative 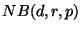 .
.