Table of Contents

The main window of Tulip software is composed of several subwindows and a menu bar :
File: this menu is used for usual file operations : New(Ctrl+N), Open(Ctrl+O), Save(Ctrl+S), Save As(Ctrl+Shift+S), Print(Ctrl+P) and Exit(Ctrl+Q). Others are added:Import: this submenu is populated by import plugins.File: Plugins allowing importation of graph files in different format such as Adjacent Matrix, gml, dot (graphviz), or tlp (tulip default file format).Graph: Plugins allowing the creation of randomly generated graphs of different types.Misc: Plugins to capture the tree structure of a file system directory, or the graph structure of a web site.
Export: this submenu is populated by export plugins allowing to save a tulip graph accordingly to a specified format. By default Tulip is able to export in GML and TLP formats.Save as picture: this last menu gives the choice between different picture formats (BMP, EPS, JPEG, PBM, PGM, PNG, PPM, SVG, XBM, XPM) in wich graphs can be exported to.
Edit: this is composed of tools : Cut(Ctrl+X), Copy(Ctrl+C), Paste(Ctrl+V) and Find(Ctrl+F), which affect the selected elements. This menu contains also: Select All(Ctrl+A), Delete selection(Del), Deselect all(Ctrl+Shift+A), Invert Selection(Ctrl+I), Create group(Ctrl+G), Create subgraph(Ctrl+Shift+G).More details on the
Findtool : The find tool has 4 options :- Replace : Replace the current selection (nodes or edges already selected).
- Add : Add the nodes (or edges) to be selected to the current selection.
- Remove : Remove nodes (or edges) from the current selection.
- Intersect : Select the intersection between the nodes (or edges) TO BE selected, and the ones from the current selection.
Algorithm: this one is divided in several parts to make a difference between the kind of algorithms you can apply. These are:Selection: this submenu is populated by 'selection' algorithms. These algorithms allows to select nodes and or edges (assign the 'viewSelection' property see Section 3, “Properties of graph” for more details) satifying some criteria. For example the 'Loop Selection' algorithm detects all edges for which the starting and ending nodes are the same.Color: this submenu is populated by 'color' algorithms. These king of algorithm computes the color (the 'viewColor' property see Section 3, “Properties of graph” for more details ) of the graph elements. A default one, 'Metric Mapping', is provided; it allows to color all graph elements according to a metric property.Measure: this submenu is populated by 'metric' algorithms. These algorithms allows to compute and assigned a value to the 'viewMetric' property of graph elements see Section 3, “Properties of graph” for more details. For example, when running the 'Degree' algorithm, the degree (the number of its neighbors) is compute and assigned to each graph node 'viewMetric' property.Layout: this submenu is populated by 'layout' algorithms which allow to display graphs using different types of drawings. For example, the 'Circular' algorithm places all nodes of a graph along a circle.Before :
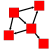
After :

Size: this submenu is populated by 'size' algorithms which allow to compute the size (the 'viewSize' property see Section 3, “Properties of graph” for more details) of the graph elements.General: this submenu is populated by more general algorithms for computing properties, subgraphs, quotient graphs, groups... For example the 'Equal Value' algorithm create subgraphs for which the included elements have the same value for a choosed 'metric' property.
For more information please visit Section 2, “Algorithms”
Graph: This menu is composed of 2 sub menus :Tests: This sub menu contains tools able to say if the graph obey some constraints :Simple:Is the Graph Simple ?
For more information please visit : Wikipedia: Simple graphs
Directed Tree:A directed tree is a directed graph which would be a tree if the directions on the edges were ignored. Some authors restrict the phrase to the case where the edges are all directed towards a particular vertex, or all directed away from a particular vertex.
For more information please visit : Wikipedia: Directed Tree
Free Tree:A tree without any designated root is called a free tree.
For more information please visit : Wikipedia: Simple graphs
Acyclic:A graph is acyclic if it contains no cycle. A cycle is a path that as the same source and target.
For more information please visit : Wikipedia: Acyclic graphs
Connected:A graph is called connected if every pair of vertices in the graph is connected. For more information please visit :
Bi-connected:A connected graph is biconnected if the removal of any single node and his out edges can not disconnect the graph.
For more information please visit :Wikipedia: Biconnected Graphs
Tri-connected:If it is always possible to establish a path from any node to an other one even after removing any 2 nodes, then the graph is said to be Tri-connected.
For more information please visit : Wikipedia: k-connected graphs
Planar: A graph is said to be planar if it can be drawn on the (Euclidean) plane without any edges crossing.
Modify: Those operations will modify the entire structure of a graph .Make Simple: This algorithm will change the graph to make it a simple graph.For more information please visit : Wikipedia: Simple graphs
Make Acyclic: A graph is acyclic if it contains no cycle. A cycle is a path that as the same source and target.For more information please visit : Wikipedia: Acyclic graphs
Make Connected: A graph is said to be connected if every pair of vertices in the graph is connected.For more information please visit : Wikipedia: Connectivity
Make Bi-connected:For more information please visit : Wikipedia: Biconnected Graphs
Make directed: If the graph is a free tree, make it directed. If a node and only one node is selected, this one will be considered as the root node. If none is selected, Tulip will heuristically choose the center of the graph as the root node. For more information please visit :- Reverse selected edges : Exchange source and target of an edge.
View: this is composed of the operations about a view. It is possible to redraw, center the current view, create a new 3D view (initially a copy of the current one) ( Section 7, “New 3D View” )Dialogs: this menu allows to redisplay each of the dialog windows such as the info editor window, or the 3D overview.Windows: this menu contains two options for the management of the views in the workspace : cascade or tile mode.Options: this menu allows to enable/disable the display options:- Force ratio : Tries to keep a good Height/Width ratio for the layout of the graph.
- Map metric : Applies the Color / Metric Mapping algorithm, whenever, a measure algorithm has been run.
- Morphing : Enables the Morphing from a layout to an other.
- Tooltips : Enables the display of tooltips on nodes or edges
- Grid : Shows the grid configuration dialog.
Help: in this menu, you can find informations about the software and the way to make your first steps.