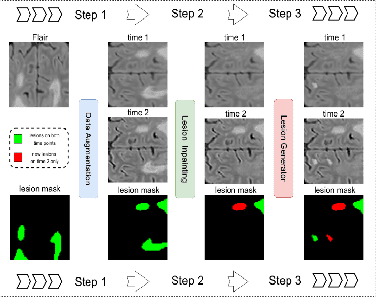
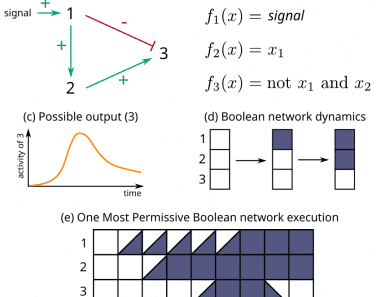
Publications, thèses, contrats et brevets
Le LaBRI contribue au développement de la recherche nationale et internationale à travers diverses activités.
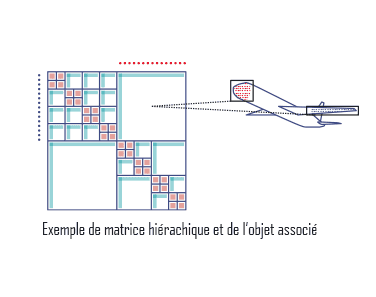
Publications
Combinatoire et Algorithme, Image et Son, Méthodes Formelles, Bioinformatique, Dataviz, Réseaux, Systèmes, etc.
Formation par la recherche
Informations générales, actualités, textes législatifs et sujets de thèses des années précédentes.
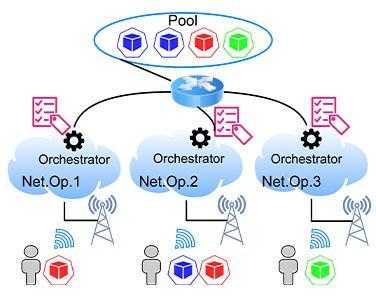
Collaborations industrielles
Contrats et relations partenariales.
Le LaBRI en chiffres
104
enseignants chercheurs
47
chercheurs
30
supports à la recherche (ITA/BIATS)
117
doctorants/post-doctorants
Une question, un projet ?
N'hésitez pas à nous contacter via ce formulaire ou par téléphone.
Vous pouvez nous contacter par téléphone :
+33 (0) 5 40 00 69 00