Publications, theses, contracts and patents
The LaBRI contributes to the development of national and international research through various activities.
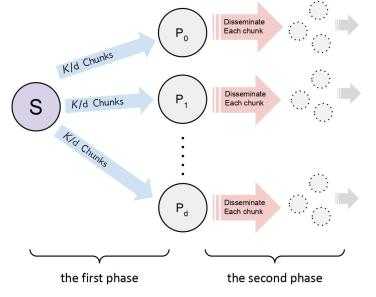
Publications
Combinatorics and Algorithms, Image and Sound, Formal Methods, Bioinformatics, Dataviz, Networks, Systems, etc.
Training through research
General information, news, legislation and thesis topics from previous years
Industrial collaborations
Contracts, European projects, milestones, partnership relations.
The LaBRI in numbers
104
teachers researchers
47
researchers
30
researcher support (ITA/BIATS)
117
PhD students/post-doctoral students
A question, a project?
Do not hesitate to contact us via this form or by phone.
You can join us by phone:
+33 (0) 5 40 00 69 00